(一)Seetaface2 基本概念

1 图像

1.1 结构定义

作为图像处理的C++库，图像存储是一个基本数据结构。
接口中图像对象为SeetaImageData。

    struct SeetaImageData
    {
    int width; // 图像宽度
    int height; // 图像高度
    int channels; // 图像通道
    unsigned char *data; // 图像数据
    };

这里要说明的是data的存储格式，其存储的是连续存放的试用8位无符号整数表示的像素值，存储为[height, width, channels]顺序。彩色图像时三通道以BGR通道排列。
如下图所示，就是展示了高4宽3的彩色图像内存格式。

Image Layout

该存储在内存中是连续存储。因此，上图中表示的图像data的存储空间为433=36bytes。

提示： BGR是OpenCV默认的图像格式。在大家很多时候看到就是直接将cv::Mat的data直接赋值给SeetaImageData的data。

data的数据类型为uint8，数值范围为[0, 255]，表示了对应的灰度值由最暗到最亮。在一些用浮点数 float表示灰度值的平台上，该范围映射到为[0, 1]。

这里详细描述格式是为了对接不同应用场景下的图像库的图像表述格式，这里注意的两点，1. 数据类型是uint8表示的[0, 255]范围；2. 颜色通道是BGR格式，而很多图像库常见的是RGB或者RGBA(A为alpha不透明度)。

提示：颜色通道会影响识别算法的精度，在不同库的转换时需要小心注意。

这种纯C接口不利于一些资源管理的情况。SeetaFace 提供给了对应SeetaImageData的封装seeta::ImageData和seeta::cv::ImageData。

1.2 使用示例

以下就是使用OpenCV加载图像后转换为SeetaImageData的操作。

    cv::Mat cvimage = cv::imread("1.jpg", cv::IMREAD_COLOR);
    SeetaImageData simage;
    simage.width = cvimage.cols;
    simage.height = cvimage.rows;
    simage.channels = cvimage.channels();
    simage.data = cvimage.data;

注意：simage.data拿到的是“借来的”临时数据，在试用的期间，必须保证cvimage的对象不被释放，或者形式的更新。
注意：原始图像可能是空的，为了输入的合法性，需要通过cvimage.empty()方法，判断图像是否为空。

这里通过cv::imread并且第二个参数设置为cv::IMREAD_COLOR，获取到的cv::Mat的图像数据是连续存储的，这个是使用SeetaImageData必须的。如果不确定是否是连续存储的对象，可以调用下述代码段进行转换。

if (!cvimage.isContinuous()) cvimage = cvimage.clone();

当然，根据cv::Mat和SeetaImageData，对象的转换可以逆向。

cv::Mat another_cvimage = cv::Mat(simage.height, simage.width, CV_8UC(simage.channels), simage.data);

seeta::ImageData和seeta::cv::ImageData也是基于这种基本的类型定义进行的封装，并加进了对象声明周期的管理。

这里展示了一种封装：

    namespace seeta
    {
    namespace cv
    {
    // using namespace ::cv;
    class ImageData : public SeetaImageData {
    public:
    ImageData( const ::cv::Mat &mat )
    : cv_mat( mat.clone() ) {
    this->width = cv_mat.cols;
    this->height = cv_mat.rows;
    this->channels = cv_mat.channels();
    this->data = cv_mat.data;
    }
    private:
    ::cv::Mat cv_mat;
    };
    }
    }

这样SeetaImageData使用代码就可以简化为：

   seeta::cv::ImageData = cv::imread("1.jpg");

因为seeta::cv::ImageData继承了SeetaImageData，因此在需要传入const SeetaImageData &类型的地方，可以直接传入seeta::cv::ImageData对象。

2. 人脸检测和关键点定位

终于经过繁杂的基础特性说明之后，迎来了两个重要的识别器模块。人脸检测和关键点定位。

人脸检测, seeta::FaceDetector 就是输入待检测的图片，输出检测到的每个人脸位置，用矩形表示。
关键点定位，seeta::FaceLandmarker就是输入待检测的图片，和待检测的人脸位置，输出N个关键点的坐标（图片内）。

两个模块分别负责找出可以处理的人脸位置，检测出关键点用于标定人脸的状态，方便后续的人脸对齐后进行对应识别分析。

2.1 人脸检测器

人脸检测器的效果如图所示：
FaceDetector

这里给出人脸检测器的主要接口：

    namespace seeta {
    class FaceDetector {
    FaceDetector(const SeetaModelSetting &setting);
    SeetaFaceInfoArray detect(const SeetaImageData &image) const;
    std::vector<SeetaFaceInfo> detect_v2(const SeetaImageData &image) const;
    void set(Property property, double value);
    double get(Property property) const;
    }
    }

构造一个检测器的函数参考如下：

    #include <seeta/FaceDetector.h>
    seeta::FaceDetector *new_fd() {
    seeta::ModelSetting setting;
    setting.append("face_detector.csta");
    return new seeta::FaceDetector(setting);
    }

有了检测器，我们就可以对图片检测人脸，检测图片中所有人脸并打印坐标的函数参考如下：

    #include <seeta/FaceDetector.h>
    void detect(seeta::FaceDetector *fd, const SeetaImageData &image) {
    std::vector<SeetaFaceInfo> faces = fd->detect_v2(image);
    for (auto &face : faces) {
    SeetaRect rect = face.pos;
    std::cout << "[" << rect.x << ", " << rect.y << ", "
    << rect.width << ", " << rect.height << "]: "
    << face.score << std::endl;
    }
    }

这里要说明的是，一般检测返回的所有人脸是按照置信度排序的，当应用需要获取最大的人脸时，可以对检测结果进行一个部分排序获取出最大的人脸，如下代码排序完成后，faces[0]就是最大人脸的位置。

    std::partial_sort(faces.begin(), faces.begin() + 1, faces.end(), [](SeetaFaceInfo a, SeetaFaceInfo b) {
    return a.pos.width > b.pos.width;
    });

人脸检测器可以设置一些参数，通过set方法。可以设置的属性有:

    seeta::FaceDetector::PROPERTY_MIN_FACE_SIZE 最小人脸
    seeta::FaceDetector::PROPERTY_THRESHOLD 检测器阈值
    seeta::FaceDetector::PROPERTY_MAX_IMAGE_WIDTH 可检测的图像最大宽度
    seeta::FaceDetector::PROPERTY_MAX_IMAGE_HEIGHT 可检测的图像最大高度

最小人脸是人脸检测器常用的一个概念，默认值为20，单位像素。它表示了在一个输入图片上可以检测到的最小人脸尺度，注意这个尺度并非严格的像素值，例如设置最小人脸80，检测到了宽度为75的人脸是正常的，这个值是给出检测能力的下限。

最小人脸和检测器性能息息相关。主要方面是速度，使用建议上，我们建议在应用范围内，这个值设定的越大越好。SeetaFace采用的是BindingBox Regresion的方式训练的检测器。如果最小人脸参数设置为80的话，从检测能力上，可以将原图缩小的原来的1/4，这样从计算复杂度上，能够比最小人脸设置为20时，提速到16倍。

检测器阈值默认值是0.9，合理范围为[0, 1]。这个值一般不进行调整，除了用来处理一些极端情况。这个值设置的越小，漏检的概率越小，同时误检的概率会提高；

可检测的图像最大宽度和可检测的图像最大高度是相关的设置，默认值都是2000。最大高度和宽度，是算法实际检测的高度。检测器是支持动态输入的，但是输入图像越大，计算所使用的内存越大、计算时间越长。如果不加以限制，一个超高分辨率的图片会轻易的把内存撑爆。这里的限制就是，当输入图片的宽或者高超过限度之后，会自动将图片缩小到限制的分辨率之内。

我们当然希望，一个算法在各种场景下都能够很好的运行，但是自然规律远远不是一个几兆的文件就是能够完全解释的。应用上总会需要取舍，也就是trade-off。

2.2 人脸关键点定位器

关键点定位器的效果如图所示：
FaceLandmarker

关键定定位输入的是原始图片和人脸检测结果，给出指定人脸上的关键点的依次坐标。

这里检测到的5点坐标循序依次为，左眼中心、右眼中心、鼻尖、左嘴角和右嘴角。
注意这里的左右是基于图片内容的左右，并不是图片中人的左右，即左眼中心就是图片中左边的眼睛的中心。

同样的方式，我们也可以构造关键点定位器：

    #include <seeta/FaceLandmarker.h>
    seeta::FaceLandmarker *new_fl() {
    seeta::ModelSetting setting;
    setting.append("face_landmarker_pts5.csta");
    return new seeta::FaceLandmarker(setting);
    }

根据人脸检测关键点，并将坐标打印出来的代码如下：

    #include <seeta/FaceLandmarker.h>
    void mark(seeta::FaceLandmarker *fl, const SeetaImageData &image, const SeetaRect &face) {
    std::vector<SeetaPointF> points = fl->mark(image, face);
    for (auto &point : points) {
    std::cout << "[" << point.x << ", " << point.y << "]" << std::endl;
    }
    }

当然开放版也会有多点的模型放出来，限于篇幅不再对点的位置做过多的文字描述。
例如face_landmarker_pts68.csta就是68个关键点检测的模型。其坐标位置可以通过逐个打印出来进行区分。

这里需要强调说明一下，这里的关键点是指人脸上的关键位置的坐标，在一些表述中也将关键点称之为特征点，但是这个和人脸识别中提取的特征概念没有任何相关性。并不存在结论，关键点定位越多，人脸识别精度越高。

一般的关键点定位和其他的基于人脸的分析是基于5点定位的。而且算法流程确定下来之后，只能使用5点定位。5点定位是后续算法的先验，并不能直接替换。从经验上来说，5点定位已经足够处理人脸识别或其他相关分析的精度需求，单纯增加关键点个数，只是增加方法的复杂度，并不对最终结果产生直接影响。

参考：seeta/FaceDetector.h seeta/FaceLandmarker.h

3. 人脸特征提取和对比

这两个重要的功能都是seeta::FaceRecognizer模块提供的基本功能。特征提取方式和对比是对应的。

这是人脸识别的一个基本概念，就是将待识别的人脸经过处理变成二进制数据的特征，然后基于特征表示的人脸进行相似度计算，最终与相似度阈值对比，一般超过阈值就认为特征表示的人脸是同一个人。

这里SeetaFace的特征都是float数组，特征对比方式是向量內积。

3.1 人脸特征提取

首先可以构造人脸识别器以备用：

    #include <seeta/FaceRecognizer.h>
    seeta::FaceRecognizer *new_fr() {
    seeta::ModelSetting setting;
    setting.append("face_recognizer.csta");
    return new seeta::FaceRecognizer(setting);
    }

特征提取过程可以分为两个步骤：1. 根据人脸5个关键点裁剪出人脸区域；2. 将人脸区域输入特征提取网络提取特征。
这两个步骤可以分开调用，也可以独立调用。

两个步骤分别对应seeta::FaceRecognizer的CropFaceV2和ExtractCroppedFace。也可以用Extract方法一次完成两个步骤的工作。

这里列举使用Extract进行特征提取的函数：

    #include <seeta/FaceRecognizer.h>
    #include <memory>
    std::shared_ptr<float> extract(
    seeta::FaceRecognizer *fr,
    const SeetaImageData &image,
    const std::vector<SeetaPointF> &points) {
    std::shared_ptr<float> features(
    new float[fr->GetExtractFeatureSize()],
    std::default_delete<float[]>());
    fr->Extract(image, points.data(), features.get());
    return features;
    }

同样可以给出相似度计算的函数：

    #include <seeta/FaceRecognizer.h>
    #include <memory>
    float compare(seeta::FaceRecognizer *fr,
    const std::shared_ptr<float> &feat1,
    const std::shared_ptr<float> &feat2) {
    return fr->CalculateSimilarity(feat1.get(), feat2.get());
    }

注意：这里points的关键点个数必须是SeetaFace提取的5点关键点。

特征长度是不同模型可能不同的，要使用GetExtractFeatureSize方法获取当前使用模型提取的特征长度。

相似度的范围是[0, 1]，但是需要注意的是，如果是直接用內积计算的话，因为特征中存在复数，所以计算出的相似度可能为负数。识别器内部会将负数映射到0。

在一些特殊的情况下，需要将特征提取分开两步进行，比如前端裁剪处理图片，服务器进行特征提取和对比。下面给出分步骤的特征提取方式：

    #include <seeta/FaceRecognizer.h>
    #include <memory>
    std::shared_ptr<float> extract_v2(
    seeta::FaceRecognizer *fr,
    const SeetaImageData &image,
    const std::vector<SeetaPointF> &points) {
    std::shared_ptr<float> features(
    new float[fr->GetExtractFeatureSize()],
    std::default_delete<float[]>());
    seeta::ImageData face = fr->CropFaceV2(image, points.data());
    fr->ExtractCroppedFace(face, features.get());
    return features;
    }

函数中间临时申请的face和features的对象大小，在识别器加载后就已经固定了，所以这部分的内存对象是可以复用的。

特别指出，如果只是对一个图像中最大人脸做特征提取的函数可以实现为：

    std::shared_ptr<float> extract(
    seeta::FaceDetector *fd,
    seeta::FaceLandmarker *fl,
    seeta::FaceRecognizer *fr,
    const SeetaImageData &image) {
    auto faces = fd->detect_v2(image);
    if (faces.empty()) return nullptr;
    std::partial_sort(faces.begin(), faces.begin() + 1, faces.end(),
    [](SeetaFaceInfo a, SeetaFaceInfo b) {
    return a.pos.width > b.pos.width;
    });
    auto points = fl->mark(image, faces[0].pos);
    return extract(fr, image, points);
    }

(二)代码实现

实现81特征点检测

/*
 * @Descripttion: 
 * @version: 
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-11-28 01:14:29
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-28 11:35:18
 */
#include <seeta/FaceDetector.h>
#include <seeta/FaceLandmarker.h>
#include <seeta/FaceRecognizer.h>
#include <seeta/Struct.h>
#include <array>
#include <map>
#include <iostream>

#ifdef __cplusplus
extern "C" {
#endif
#include "cv.h"
#include "li_image.h"
#include "li_painter.h"
#ifdef __cplusplus
}
#endif

int test_image(seeta::FaceDetector &FD, seeta::FaceLandmarker &FL)
{
    for(int i=1;i<=4;i++){
    std::string image_path = std::to_string(i)+".bmp";
    std::cout << "Loading image: " << image_path << std::endl;
    Li_Image* img=Li_Load_Image((BYTE*)image_path.c_str(),BMP_888);
    Li_Image* square=Li_ReShape(img,500,500);
    Li_Image* img2=Li_Rotate(square);
    Li_Image* img1=Li_Convert_Image(img2,LI_BMP_888_2_LI_BMP_8);

    SeetaImageData simage;
    simage.width=img1->width;
    simage.height=img1->height;
    simage.data=(unsigned char*)img1->data;
    simage.channels=1;

    auto faces = FD.detect(simage);

    std::cout<<faces.size<<std::endl;
    for (int i = 0; i < faces.size; ++i)
    {
        auto &face = faces.data[i];
        auto points = FL.mark(simage, face.pos);

        Li_Line(img2,0xFF0000,face.pos.x,face.pos.y,face.pos.x,face.pos.y+face.pos.height);
        Li_Line(img2,0xFF0000,face.pos.x,face.pos.y,face.pos.x+face.pos.width,face.pos.y);
        Li_Line(img2,0xFF0000,face.pos.x+face.pos.width,face.pos.y,face.pos.x+face.pos.width,face.pos.y+face.pos.height);
        Li_Line(img2,0xFF0000,face.pos.x,face.pos.y+face.pos.height,face.pos.x+face.pos.width,face.pos.y+face.pos.height);
        for (auto &point : points)
        {
            Li_Circle(img2,0xFF0000,point.x,point.y,1);
        }
    }
    Li_Image*res= Li_Rotate(img2);
    auto output_path = image_path + ".pts81.bmp";
    Li_Save_Image((BYTE*)output_path.c_str(),res);
    std::cerr << "Saving result into: " << output_path << std::endl;
    }
    return EXIT_SUCCESS;
}

int main()
{
    seeta::ModelSetting::Device device = seeta::ModelSetting::CPU;
    int id = 0;
    seeta::ModelSetting FD_model( "./model/fd_2_00.dat", device, id );
    seeta::ModelSetting FL_model( "./model/pd_2_00_pts81.dat", device, id );

    seeta::FaceDetector FD(FD_model);
    seeta::FaceLandmarker FL(FL_model);


    FD.set(seeta::FaceDetector::PROPERTY_VIDEO_STABLE, 1);

    return test_image(FD, FL);

}

(三)效果

(四)写在后面

代码中有错误的地方还望指出。我已经将项目同步到了github，我会实时更新这个代码仓库。
项目github地址：
LiteCV

2021年7月6日2021年7月6日

(一)关于QR二维码

一：什么是二维码

二维码（2-dimensional bar code）是用某种特定的几何图形按一定规律在平面（二维方向上）分布的黑白相间的图形记录数据符号信息的。在许多种类的二维条码中，常用的码制有：Data Matrix, Maxi Code, Aztec, QR Code, Vericode, PDF417, Ultracode, Code 49, Code 16K等。
1.堆叠式/行排式二维条码，如，Code 16K、Code 49、PDF417
2.矩阵式二维码，最流行莫过于QR CODE 二维码的名称是相对与一维码来说的，比如以前的条形码就是一个“一维码”，它的优点有：二维码存储的数据量更大；可以包含数字、字符，及中文文本等混合内容；有一定的容错性（在部分损坏以后可以正常读取）；空间利用率高等。

二：什么是QR二维码

QR(Quick-Response) code是被广泛使用的一种二维码，解码速度快。由DENSO(日本电装)公司开发，由JIS和ISO将其标准化。
QR码呈正方形，只有黑白两色。在3个角落，印有较小，像「回」字的的正方图案。这三个是帮助解码软件定位的图案，使用者不需要对准，无论以任何角度拍摄，内容仍可正确被读取。

三：将数据编码成QR码的流程

数据分析：确定编码的字符类型，按相应的字符集转换成符号字符；选择纠错等级，在规格一定的条件下，纠错等级越高其真实数据的容量越小。
数据编码：将数据字符转换为位流，每8位一个码字，整体构成一个数据的码字序列。其实知道这个数据码字序列就知道了二维码的数据内容。

数据可以按照一种模式进行编码，以便进行更高效的解码，例如：对数据：01234567编码（版本1-H）， 1）分组：012 345 67 2）转成二进制：012→0000001100 345→0101011001 67 →1000011 3）转成序列：0000001100 0101011001 1000011 4）字符数 转成二进制：8→0000001000 5）加入模式指示符（上图数字）0001：0001 0000001000 0000001100 0101011001 1000011 对于字母、中文、日文等只是分组的方式、模式等内容有所区别。基本方法是一致的
纠错编码：按需要将上面的码字序列分块，并根据纠错等级和分块的码字，产生纠错码字，并把纠错码字加入到数据码字序列后面，成为一个新的序列。

在二维码规格和纠错等级确定的情况下，其实它所能容纳的码字总数和纠错码字数也就确定了，比如：版本10，纠错等级时H时，总共能容纳346个码字，其中224个纠错码字。 就是说二维码区域中大约1/3的码字时冗余的。对于这224个纠错码字，它能够纠正112个替代错误（如黑白颠倒）或者224个据读错误（无法读到或者无法译码）， 这样纠错容量为：112/346=32.4%
构造最终数据信息：在规格确定的条件下，将上面产生的序列按次序放如分块中 按规定把数据分块，然后对每一块进行计算，得出相应的纠错码字区块，把纠错码字区块 按顺序构成一个序列，添加到原先的数据码字序列后面。 如：D1, D12, D23, D35, D2, D13, D24, D36, … D11, D22, D33, D45, D34, D46, E1, E23,E45, E67, E2, E24, E46, E68，…
构造矩阵：将探测图形、分隔符、定位图形、校正图形和码字模块放入矩阵中。
把上面的完整序列填充到相应规格的二维码矩阵的区域中
掩摸：将掩摸图形用于符号的编码区域，使得二维码图形中的深色和浅色（黑色和白色）区域能够比率最优的分布。 一个算法，不研究了，有兴趣的同学可以继续。
格式和版本信息：生成格式和版本信息放入相应区域内。 版本7-40都包含了版本信息，没有版本信息的全为0。二维码上两个位置包含了版本信息，它们是冗余的。 版本信息共18位，6X3的矩阵，其中6位时数据为，如版本号8，数据位的信息时 001000，后面的12位是纠错位。

(二)编译QRencode

libqrencode 可以使用cmake 进行编译
Linux:

cmake ..
make

Windows:

cmake .. -G "MinGW Makefiles"
mingw32-make.exe

(三)使用libqrencode.a

/*
 * @Descripttion: 二维码编码
 * @version: V 1.0
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-11-26 11:43:15
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-26 18:01:26
 */
#include <string.h>
#include "qrencode.h"  
#include "cv.h"
#include "li_image.h"
#include "li_qrcode.h"

/**
 * @name: Li_QREncode
 * @msg: 二维码生成
 * @param {BYTE* src字符串}
 * @return {Li_Image*}
 */
Li_Image* Li_QREncode(BYTE* src)
{
    QRcode*  pQRC;
    int unWidth, unWidthAdjusted, unDataBytes;
    Li_Image* out;
    BYTE* pSourceData,*pDestData,*pRGBData ;
    if (pQRC = QRcode_encodeString(src, 0, QR_ECLEVEL_H, QR_MODE_8, 1))
    {
        unWidth=pQRC->width;
                unWidthAdjusted = unWidth * 8 * 3;
        if (unWidthAdjusted % 4)
            unWidthAdjusted = (unWidthAdjusted / 4 + 1) * 4;
        unDataBytes = unWidthAdjusted * unWidth * 8;
        out=Li_Create_Image(8*unWidth,8*unWidth,LI_DEP_24U,LI_BMP_888);
        pSourceData = pQRC->data;
        pRGBData=out->data;
        pSourceData = pQRC->data;
        for (int y = 0; y < unWidth; y++)
        {
            pDestData = pRGBData + unWidthAdjusted * y * 8;
            for (int x = 0; x < unWidth; x++)
            {
                if (*pSourceData & 1)
                {
                    for (int l = 0; l < 8; l++)
                    {
                        for (int n = 0; n < 8; n++)

                        {
                             //以下三行是设置三基色，三基色都设置为0x00，则生成的二维码图片就是黑色的了，要什么颜色自己调整
                            *(pDestData + n * 3 + unWidthAdjusted * l) = 0x00;            
                            *(pDestData + 1 + n * 3 + unWidthAdjusted * l) = 0x00;
                            *(pDestData + 2 + n * 3 + unWidthAdjusted * l) = 0x00;
                        }
                    }
                }
                pDestData += 3 * 8;
                pSourceData++;
            }
        }
    }
    return out;
}

/*
 * @Descripttion: 
 * @version: 
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-11-26 12:23:49
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-26 15:04:58
 */
#include "cv.h"
#include "li_image.h"
#include "li_qrcode.h"

int main()
{
    Li_Image* Qr=Li_QREncode("123.57.93.3");
    Li_Save_Image("QR.bmp",Qr);

    LILOG("OVER");
}

(四)效果

(五)写在后面

代码中有错误的地方还望指出。我已经将项目同步到了github，我会实时更新这个代码仓库。
项目github地址：
LiteCV

2021年7月6日2021年7月6日

【数字图像处理】Hough变换C语言实现

@[TOC]

(一)Hough圆检测

经过图像的预处理后，我们得到了只保留边缘信息的二值图像，统计可以发现在一个320×240的图像中最后有效的信息点只有5000个左右现在就是通过对这5000个点的统计与运算完成对圆与直线的检测。直线检测最容易受到环境干扰，如果直接对一幅图像进行直线检测，检测出最长的那根直线不一定，是你想要的直线。所以我们首先要进行的是Hough圆的检测。
Hough变换不仅适用于直线检测，还适用于任何形式的f(x,a)=0所表示的图形的检测，其中x 表示坐标向量，a表示系数向量。下边我们对Hough变换检测圆的原理做简要介绍。
对于一个半径为r，圆心为（a,b）的圆，我们将其表示为：

此时x=[x,y]T，a=[a,b,r]T，其参数空间为三维。
显然，图像空间上的一点（x,y），在参数空间中对应着一个圆锥，如下图所示。

而图像空间的一个圆就对应着这一簇圆锥相交的一个点，这个特定点在参数空间的三维参数一定，就表示一定半径一定圆心坐标的图像空间的那个圆。
上述方法是经典的Hough圆检测方法的原理，它具有精度高，抗干扰能力强等优点，但由于该方法的参数空间为三维，要在三维空间上进行证据累计的话，需要的时间和空间都是庞大的，在实际应用中不适用。

程序设计

Hough变换的具体算法步骤如下：
• 适当的量化参数空间。
• 将参数空间的每一个单元看作一个累加器。
• 初始化累加器为0。
• 对图像空间的每一点，在其所满足参数方程对应的累加器上加1。
• 累加器存储的最大值即为对应的图形的参数。

程序实际思路：

（1）因为如果直接进行Hough圆的投票的话，我们需要一个3维的表保存行，列，角度信息。我们将这个投票过程分成两个步骤。

（2）首先完成对于固定半径的圆的投票。然后在对每一个半径的圆的投票进行比较。

1）建立一张与原图大小一致的投票表，用来表示每个点作为圆心会有多少个点与之匹配：

    int AccuArrLength=img->width * img->height;;
    pAccumulateArr=(int*)malloc(AccuArrLength*sizeof(int));

2）在根据极坐标运算公式，对每一个点可能对应的圆心进行投票，通过遍历每一个点，然后对经过这个点所有的圆的圆心位置进行一次计票

int x = i - R * cos(theta);//得到理想圆心x坐标
int y = j - R * sin(theta);//得到理想圆心y坐标
 if(x>0&&x<img->width&&y>0&&y<img->height&&x<range[1]&&x>range[0]&&y<range[3]&&y>range[2])
 {
      pAccumulateArr[y * img->width + x]++;
  }

3）找到对应票数最高的圆心位置

    for(int i = 0; i < img->height; i++)
        for(int j = 0; j < img->width; j++)
        {
            int value_ = pAccumulateArr[i * img->width + j];
            if(value_>max_value)
            {
                //printf("(%d,%d,%d,%d)",max_value,value_,i,j);
               max_value=value_;
                circles->x=j;
                circles->y=i;
                circles->r=R;
            }
        }

然后我们就可以找到想要的圆了。

（3）对一个半径范围内的所有圆进行一次（1）中的操作，然后，从中选取票数最高的圆，那么这个圆就是我们想要的圆了。

（4）具体程序请参考Litecv/Imgproc/li_canny.c

(二) Hough直线检测

Hough变换的方法基本思想可以从检测图像中的直线这个简单问题中看到。直线由两点A=(X1,Y1)和B=(X2,Y2)定义，所下图1(a)示。通过点A的所有直线由y1=kx1+q表示，k和q是某些值。这意味着同一个方程可以解释为参数空间k,q的方程。因此通过点A的所须直线可以表示为方程q=-x1k+y1图1.(b)。类似地通过点B的直线可以表示q=-x2*k+y2。在参数空间k和q中，两条直线的唯一公共点是在原图像空间中表示连接点A和B的唯一存在的直线。

这意味着图像中的每条直线在参数空k,q中由单独一个点表示，直线的任何一部分都变换为同一个点。直线检测的主要思想是确定图中所在的直线像素，将通过这些像素的所在直线变换到参数空间的对应点，在参数空间检测点（a,b),此点是图像中出现的直线y=ax+b的Hough变换的结果。
我们可以注意到直线的参数方程y =kx+q只适合解释Hough变换原理，在检测垂直线条和参数的非线性离散化时会遇到困难。如果直线表示成s=xcosθ+ysinθ。Hough变换就没有这些局限性。直线还是被变换为单个点，因此可用该原理进行直线检测。如下图2所示：

我们要注意到Hough变换的重要性质是对图像中直线的殘缺部分、噪声以及其它共存的非直线结构不敏感。因为从图像空间到累计空间的变换的鲁棒性引起的，直线殘缺的部分只会造成较低的局部极值。

(三)代码实现

#ifndef LI_CANNY_C
#define LI_CANNY_C




#include "cv.h"
#include "li_image_proc.h"
#include <stdio.h>
#include <math.h>


/**
 * @name: Li_Canny
 * @msg:  参考文章 https://blog.csdn.net/HUSTER_Gy/article/details/102942452?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522160498444419724838560446%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=160498444419724838560446&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v28-11-102942452.first_rank_ecpm_v3_pc_rank_v2&utm_term=canny%E8%BE%B9%E7%BC%98%E6%A3%80%E6%B5%8B%E7%AE%97%E6%B3%95c%E5%AE%9E%E7%8E%B0&spm=1018.2118.3001.4449
 *        图像砍尼检测
 * @param {Li_Image* img 原图像
 *         BYTE CannyType选择算子
 *         BYTE min      最大阈值
 *         BYTE max}     最小阈值
 * @return {*}
 */
LI_API
Li_Image* Li_Canny(Li_Image* img,BYTE CannyType,BYTE min,BYTE max)
{
    if(img==NULL||img->imgdepth!=LI_DEP_8U)return NULL;
    LILOG("CANNY");           
    Li_Image* out =Li_Copy_Image(img); 
    Li_Image* PP =Li_Copy_Image(img); 
    Li_Image* QQ =Li_Copy_Image(img);
    Li_Kernel* SX,*SY;
    double *P =(double*)malloc(sizeof(double)*img->width*img->height);/*x方向偏导*/
    double *Q =(double*)malloc(sizeof(double)*img->width*img->height); /*y方向偏导*/
    /*PI*-1/2* --  PI*1/2*/
    double *Threa =(double*)malloc(sizeof(double)*img->width*img->height);

    #ifdef DEBUG
    Li_Save_Image("before_minus.bmp",out);
    #endif 

    /*开始计算梯度与方向角*/
    switch (CannyType)
    {
    case LI_CANNY_MYDEFINE:
        {
            for(int i=0;i<img->height-1;i++)
                for(int j=0;j<img->width-1;j++)
                {
                    BYTE* ptr[4];
                    BYTE* ptr2;
                    /**
                     * 2  3
                     * 0  1
                    */
                    ptr[0]=img->at(img,j,i);
                    ptr[1]=img->at(img,j+1,i);
                    ptr[2]=img->at(img,j,i+1);
                    ptr[3]=img->at(img,j+1,i+1);
                    P[i*img->width+j]=(double)((double)*ptr[3]+*ptr[1]-*ptr[0]-*ptr[2])/2;
                    Q[i*img->width+j]=(double)((double)*ptr[0]+*ptr[1]-*ptr[2]-*ptr[3])/2;  
                    Threa[i*img->width+j]=atan(Q[i*img->width+j]/P[i*img->width+j]);
                    ptr2=out->at(out,j,i);
                    *ptr2=sqrt(P[i*img->width+j]*P[i*img->width+j]+Q[i*img->width+j]*Q[i*img->width+j]);
                }
        }
        break;

    case LI_CANNY_SOBEL:
        {
            for(int i=1;i<img->height-1;i++)
                for(int j=1;j<img->width-1;j++)
                {
                    BYTE* ptr[9];
                    BYTE* ptr2;
                    /**6  7  8
                     * 3  4  5
                     * 0  1  2
                     */
                    if(j-1>=0&&i-1>=0)
                    ptr[0]=(BYTE*)img->at(img,j-1,i-1);
                    if(j>=0&&i-1>=0)
                    ptr[1]=(BYTE*)img->at(img,j+0,i-1);
                    if(j+1<=img->width&&i-1>=0)
                    ptr[2]=(BYTE*)img->at(img,j+1,i-1);
                    if(j-1>=0&&i>=0)
                    ptr[3]=(BYTE*)img->at(img,j-1,i+0);
                    if(j>=0&&i>=0)
                    ptr[4]=(BYTE*)img->at(img,j+0,i+0);
                    if(j+1<=img->width&&i>=0)
                    ptr[5]=(BYTE*)img->at(img,j+1,i+0);
                    if(j-1>=0&&i+1<=img->height)
                    ptr[6]=(BYTE*)img->at(img,j-1,i+1);
                    if(j>=0&&i+1<=img->height)
                    ptr[7]=(BYTE*)img->at(img,j+0,i+1);
                    if(j+1<=img->width&&i+1<=img->height)
                    ptr[8]=(BYTE*)img->at(img,j+1,i+1);

                    P[i*img->width+j]=(double)((double)*ptr[2]+*ptr[5]*2+*ptr[8]-*ptr[0]-*ptr[3]*2-*ptr[6]);
                    Q[i*img->width+j]=(double)((double)*ptr[6]+*ptr[7]*2+*ptr[8]-*ptr[0]-*ptr[1]*2-*ptr[2]);    
                    Threa[i*img->width+j]=atan(Q[i*img->width+j]/P[i*img->width+j]);
                    ptr2=out->at(out,j,i);
                    *ptr2=sqrt(P[i*img->width+j]*P[i*img->width+j]+Q[i*img->width+j]*Q[i*img->width+j]);
                }
        }
        break;

        case LI_CANNY_ROBERTS:
         {
            for(int i=0;i<img->height-1;i++)
                for(int j=0;j<img->width-1;j++)
                {
                    BYTE* ptr[4];
                    BYTE* ptr2;
                    /**
                     * 2  3
                     * 0  1
                    */
                    ptr[0]=img->at(img,j,i);
                    ptr[1]=img->at(img,j+1,i);
                    ptr[2]=img->at(img,j,i+1);
                    ptr[3]=img->at(img,j+1,i+1);
                    ptr2=out->at(out,j,i);
                    *ptr2=abs(*ptr[2]-*ptr[1])+abs(*ptr[0]-*ptr[3]);
                    Threa[i*img->width+j]=atan(abs(*ptr[2]-*ptr[1])/abs(*ptr[0]-*ptr[3]));
                }         
         }
        break;

    case LI_CANNY_PREWITT:
          {
            for(int i=1;i<img->height-1;i++)
                for(int j=1;j<img->width-1;j++)
                {
                    BYTE* ptr[9];
                    BYTE* ptr2;
                    /**6  7  8
                     * 3  4  5
                     * 0  1  2
                     */
                    if(j-1>=0&&i-1>=0)
                    ptr[0]=(BYTE*)img->at(img,j-1,i-1);
                    if(j>=0&&i-1>=0)
                    ptr[1]=(BYTE*)img->at(img,j+0,i-1);
                    if(j+1<=img->width&&i-1>=0)
                    ptr[2]=(BYTE*)img->at(img,j+1,i-1);
                    if(j-1>=0&&i>=0)
                    ptr[3]=(BYTE*)img->at(img,j-1,i+0);
                    if(j>=0&&i>=0)
                    ptr[4]=(BYTE*)img->at(img,j+0,i+0);
                    if(j+1<=img->width&&i>=0)
                    ptr[5]=(BYTE*)img->at(img,j+1,i+0);
                    if(j-1>=0&&i+1<=img->height)
                    ptr[6]=(BYTE*)img->at(img,j-1,i+1);
                    if(j>=0&&i+1<=img->height)
                    ptr[7]=(BYTE*)img->at(img,j+0,i+1);
                    if(j+1<=img->width&&i+1<=img->height)
                    ptr[8]=(BYTE*)img->at(img,j+1,i+1);

                    P[i*img->width+j]=(double)((double)*ptr[2]+*ptr[5]+*ptr[8]-*ptr[0]-*ptr[3]-*ptr[6]);
                    Q[i*img->width+j]=(double)((double)*ptr[6]+*ptr[7]+*ptr[8]-*ptr[0]-*ptr[1]-*ptr[2]); 
                    Threa[i*img->width+j]=atan(Q[i*img->width+j]/P[i*img->width+j]);   
                    ptr2=out->at(out,j,i);
                    *ptr2=sqrt(P[i*img->width+j]*P[i*img->width+j]+Q[i*img->width+j]*Q[i*img->width+j]);
                }
        }      

        break;

    default:
        break;
    }

    #ifdef DEBUG
    Li_Save_Image("after_minus.bmp",out);
    #endif 

    /*非极大值抑制*/
    for(int j=1;j<out->height-1;j++)
        for(int i=1;i<out->width-1;i++)
        {
            double t=Threa[j*img->width+i];
            BYTE* ptr=out->at(out,i,j);
            double g=(double) *ptr;
            double g0, g1;
            if ((t >= -(3*M_PI/8)) && (t < -(M_PI/8)))
            {
                ptr=out->at(out,i-1,j-1);
                 g0=(double) *ptr;
                ptr=out->at(out,i+1,j+1);
                 g1=(double) *ptr;
            } 
            else if ((t >= -(M_PI/8)) && (t < M_PI/8))
            {
                ptr=out->at(out,i-1,j);
                 g0=(double) *ptr;
                ptr=out->at(out,i+1,j);
                 g1=(double) *ptr;
            }
            else if ((t >= M_PI/8) && (t < 3*M_PI/8))
            {
                ptr=out->at(out,i+1,j-1);
                 g0=(double) *ptr;
                ptr=out->at(out,i-1,j+1);
                 g1=(double) *ptr;
            }
            else
            {
                ptr=out->at(out,i,j-1);
                 g0=(double) *ptr;
                ptr=out->at(out,i,j+1);
                 g1=(double) *ptr;                
            }

            if (g <= g0 || g <= g1) {
                ptr=out->at(out,i,j);
                *ptr=0;
            }

        }

    /*阈值化操作*/
    #ifdef DEBUG
    Li_Save_Image("before_thre.bmp",out);
    #endif 
    Li_Image*out1=Li_Double_Threshold(out,min,max);
    #ifdef DEBUG
    Li_Save_Image("after_thre.bmp",out1);
    #endif 

    /*边缘链接*/
        for (int j = 1; j < out1->height-2; j++) 
        for (int i = 1; i < out1->width-2; i++) {
            BYTE* ptr=out1->at(out1,i,j);
            if(*ptr==255)
            {
                for (int m = -1; m < 1; m++) {
                    for (int n = -1; n < 1; n++) {
                    BYTE* temp=out1->at(out1,i+n,j+m);
                        if(*ptr!=0&&*ptr!=255)
                        *ptr=255;
                    }
                }             
            }
        }

        for (int j = 0; j < out1->height-1; j++) {
        for (int i = 0; i < out1->width-1; i++) {
            // 如果该点依旧是弱边缘点，及此点是孤立边缘点
             BYTE* ptr=out1->at(out1,i,j);
             if(*ptr!=255&&*ptr!=0)
             *ptr=0;
            }
        }
    Li_Destroy_Image(PP);
    Li_Destroy_Image(QQ);
    return out1;
}

#endif // !LI_CANNY_C

(四)效果展示

(五)写在后面

因为LiteCV项目才刚刚写了一个开头，代码中有错误的地方还望指出。我已经将项目同步到了github，我会实时更新这个代码仓库。
项目github地址：
LiteCV

2021年7月6日2021年7月6日

【数字图像处理】Canny边缘检测C语言实现

@[TOC]

（一）边缘检测步骤

对于边缘检测我们通常需要完成的事情有：
## 1. 彩色图像转换为灰度图像
## 2. 对图像进行高斯模糊
## 3. 计算图像梯度，根据梯度计算图像边缘幅值与角度（这里其实用到了微分边缘检测算子来计算梯度幅值方向）
## 4. 非最大信号压制处理（边缘细化）
## 5. 双阈值边缘连接处理
## 6. 二值化图像输出结果

（二）图像的梯度与方向角计算

边缘检测的第一步就是计算图像的梯度与方向角。并在此基础上计算出每一个在X,Y方向梯度确定的情况下的幅值。
图像梯度是指图像某像素在x和y两个方向上的变化率（与相邻像素比较），是一个二维向量，由2个分量组成，X轴的变化、Y轴的变化。
其中X轴的变化是指当前像素右侧（X加1）的像素值减去当前像素左侧（X减1）的像素值。
同理，Y轴的变化是当前像素下方（Y加1）的像素值减去当前像素上方（Y减1）的像素值。
计算出来这2个分量，形成一个二维向量，就得到了该像素的图像梯度。取反正切arctan，可得到梯度角度。
这个求图像梯度的过程可以通过一个卷积核来实现：以[-1,0,1]为例

图像梯度的绝对值为

图像梯度的角度为

在此基础上图像处理的专家们又研究出了多种可以计算梯度的算子。常见边缘检测算子：Roberts 、Sobel 、Prewitt、Laplacian、Log/Marr、Canny、Kirsch、Nevitia。这里我们以Roberts 、Sobel 、Prewitt来分别实现。图像的梯度运算。
Robert算子是第一个边缘检测算子，提出者Lawrence Roberts in 1963。
Sobel边缘算子，当年作者并没有公开发表过论文，仅仅是在一次博士生课题讨论会(1968)上提出(“A 3×3 Isotropic Gradient Operator for Image Processing”)，后在1973年出版的一本专著（”Pattern Classification and Scene Analysis”）的脚注里作为注释出现和公开的。提出者Irwin Sobel。
Prewitt算子来自J.M.S. Prewitt “Object Enhancement and Extraction” in “Picture processing and Psychopictorics”, Academic Press,1970。
我们看这三种边缘检测算子模板及写成差分的形式：

根据以上公式可以确定梯度与角度的计算方式，下面以sobel算子为例：
33 Sobel两个方向的算子在图像上滑动，模板与其覆盖的图像33区域9个像素进行卷积，求和后得到此方向的边缘检测幅值。

f(x,y)为图像，Gx和Gy分别是水平和竖直方向算子的卷积结果，G则是最终得到的边缘幅值，θ值则是边缘方向。

下面我们来这常见的几种卷积核进行比较（example/canny/canny.c）:

（1）sobel算子

（2） Prewitt算子

（3） Robert算子

（4）三种算子效果比较

Roberts算子对具有陡峭低噪声的图像处理效果很好，但是利用Roberts算子提取边缘的结果比较粗，因此对于边缘的定位不会非常准确。
Sobel 算子对灰度渐变和噪声较多的图像处理效果比较好，Sobel算子对边缘定位比较准确。
Prewitt算子对灰度渐变和噪声较多的图像处理效果较好
综上我们选择Sobel算子作为我们的梯度运算方法。

（三）非极大值抑制

canny算子中非最大抑制(Non-maximum suppression)是回答这样一个问题: “当前的梯度值在梯度方向上是一个局部最大值吗?” 所以,要把当前位置的梯度值与梯度方向上两侧的梯度值进行比较。
非极大值抑制可以帮助抑制除局部最大值之外的所有梯度值(通过将它们设置为0) ,使其指示具有最强烈的强度值变化的位置。以目标检测为例,目标检测的过程中在同一目标的位置上会产生大量的候选框,这些候选框相互之间可能会有重叠,此时我们需要利用非极大值抑制找到最佳的目标边界框,消除冗余的边界框。
在John Canny提出的Canny算子的论文中，非最大值抑制就只是在0、90、45、135四个梯度方向上进行的，每个像素点梯度方向按照相近程度用这四个方向来代替。这种情况下，非最大值抑制所比较的相邻两个像素就是：
1） 0：左边和右边
2）45：右上和左下
3）90：上边和下边
4）135：左上和右下

这样做的好处是简单，但是这种简化的方法无法达到最好的效果，因为，自然图像中的边缘梯度方向不一定是沿着这四个方向的。因此，就有很大的必要进行插值，找出在一个像素点上最能吻合其所在梯度方向的两侧的像素值。
然而，实际数字图像中的像素点是离散的二维矩阵，所以处在真正中心位置C处的梯度方向两侧的点是不一定存在的，或者说是一个亚像素(sub pixel)点，而这个不存在的点，以及这个点的梯度值就必须通过对其两侧的点进行插值来得到。
步骤：

对角度在四个方向进行划分，形成新的角度图；
根据角度图(表征着梯度的方向)，对幅值进行非极大值抑制。
以3X3图像为例，按下图进行比较。

非极大值抑制效果：

图表 13 非极大值抑制
可以看到大量的非边缘点被过滤掉了。

（四）图像双阈值化与边缘连接

对于一些图像有很强的分界特征，我们可以考虑用双阈值法进行二值化操作。
双阈值化思想：

首先要确定的是该方法同样也是对灰度图进行操作。
然后，我们预设两个特定的阈值量thresh1、thresh2，并且thresh1 < thresh2 。
阈值化的过程就是，将在（thresh1，thresh2）这个区间内的灰度值设置为maxVal，将其余部分设置为0
双阈值化操作中的两个预设阈值量根据实际需要自行设置，需要说明的是，maxVal可以是某一个固定值（通常情况下8位无符号图像设置为最大灰度值255）。
双阈值化类型如下式所示：

在3.3.2中已经完成了很大一部分点的过滤，但是含有很多的弱边缘点就是说他们的幅值达不到要求，这个时候我们就需要想办法过滤掉这些幅值达不到要求的点。

步骤：
• 选取高阈值 T H 和低阈值 T L ，比率为 2 : 1 或 3 : 1 。（一般取 T H = 0.3 / 0.2 , T L = 0.1 T_H和低阈值T_L，比率为2:1或3:1。（一般取T_H=0.3/0.2,T_L=0.1 TH和低阈值TL，比率为2:1或3:1。（一般取TH=0.3/0.2,TL=0.1）
• 取出非极大值抑制后的图像中的最大梯度幅值，重新定义高低阈值。即： T H × M a x , T L × M a x T_H\times{Max},T_L\times{Max} TH×Max,TL×Max。(当然可以自己给定)
• 将小于 T L 的点抛弃，赋 0 ；将大于 T H 的点立即标记（这些点就是边缘点），赋 1 。将小于T_L的点抛弃，赋0；将大于T_H的点立即标记（这些点就是边缘点），赋1。将小于TL的点抛弃，赋0；将大于TH的点立即标记（这些点就是边缘点），赋1。
• 将大于 T L ，小于 T H 的点使用 8 连通区域确定（即：只有与 T H 像素连接时才会被接受，成为边缘点，赋 1 ）将大于T_L，小于T_H的点使用8连通区域确定（即：只有与T_H像素连接时才会被接受，成为边缘点，赋1）将大于TL，小于TH的点使用8连通区域确定（即：只有与TH像素连接时才会被接受，成为边缘点，赋1）
效果如下：

可以看到很多若边缘点被进一步的过滤掉。

（五）代码实现

li_canny.c

#ifndef LI_CANNY_C
#define LI_CANNY_C




#include "cv.h"
#include "li_image_proc.h"
#include <stdio.h>
#include <math.h>


/**
 * @name: Li_Canny
 * @msg:  参考文章 https://blog.csdn.net/HUSTER_Gy/article/details/102942452?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522160498444419724838560446%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=160498444419724838560446&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v28-11-102942452.first_rank_ecpm_v3_pc_rank_v2&utm_term=canny%E8%BE%B9%E7%BC%98%E6%A3%80%E6%B5%8B%E7%AE%97%E6%B3%95c%E5%AE%9E%E7%8E%B0&spm=1018.2118.3001.4449
 *        图像砍尼检测
 * @param {Li_Image* img 原图像
 *         BYTE CannyType选择算子
 *         BYTE min      最大阈值
 *         BYTE max}     最小阈值
 * @return {*}
 */
LI_API
Li_Image* Li_Canny(Li_Image* img,BYTE CannyType,BYTE min,BYTE max)
{
    if(img==NULL||img->imgdepth!=LI_DEP_8U)return NULL;
    LILOG("CANNY");           
    Li_Image* out =Li_Copy_Image(img); 
    Li_Image* PP =Li_Copy_Image(img); 
    Li_Image* QQ =Li_Copy_Image(img);
    Li_Kernel* SX,*SY;
    double *P =(double*)malloc(sizeof(double)*img->width*img->height);/*x方向偏导*/
    double *Q =(double*)malloc(sizeof(double)*img->width*img->height); /*y方向偏导*/
    /*PI*-1/2* --  PI*1/2*/
    double *Threa =(double*)malloc(sizeof(double)*img->width*img->height);

    #ifdef DEBUG
    Li_Save_Image("before_minus.bmp",out);
    #endif 

    /*开始计算梯度与方向角*/
    switch (CannyType)
    {
    case LI_CANNY_MYDEFINE:
        {
            for(int i=0;i<img->height-1;i++)
                for(int j=0;j<img->width-1;j++)
                {
                    BYTE* ptr[4];
                    BYTE* ptr2;
                    /**
                     * 2  3
                     * 0  1
                    */
                    ptr[0]=img->at(img,j,i);
                    ptr[1]=img->at(img,j+1,i);
                    ptr[2]=img->at(img,j,i+1);
                    ptr[3]=img->at(img,j+1,i+1);
                    P[i*img->width+j]=(double)((double)*ptr[3]+*ptr[1]-*ptr[0]-*ptr[2])/2;
                    Q[i*img->width+j]=(double)((double)*ptr[0]+*ptr[1]-*ptr[2]-*ptr[3])/2;  
                    Threa[i*img->width+j]=atan(Q[i*img->width+j]/P[i*img->width+j]);
                    ptr2=out->at(out,j,i);
                    *ptr2=sqrt(P[i*img->width+j]*P[i*img->width+j]+Q[i*img->width+j]*Q[i*img->width+j]);
                }
        }
        break;

    case LI_CANNY_SOBEL:
        {
            for(int i=1;i<img->height-1;i++)
                for(int j=1;j<img->width-1;j++)
                {
                    BYTE* ptr[9];
                    BYTE* ptr2;
                    /**6  7  8
                     * 3  4  5
                     * 0  1  2
                     */
                    if(j-1>=0&&i-1>=0)
                    ptr[0]=(BYTE*)img->at(img,j-1,i-1);
                    if(j>=0&&i-1>=0)
                    ptr[1]=(BYTE*)img->at(img,j+0,i-1);
                    if(j+1<=img->width&&i-1>=0)
                    ptr[2]=(BYTE*)img->at(img,j+1,i-1);
                    if(j-1>=0&&i>=0)
                    ptr[3]=(BYTE*)img->at(img,j-1,i+0);
                    if(j>=0&&i>=0)
                    ptr[4]=(BYTE*)img->at(img,j+0,i+0);
                    if(j+1<=img->width&&i>=0)
                    ptr[5]=(BYTE*)img->at(img,j+1,i+0);
                    if(j-1>=0&&i+1<=img->height)
                    ptr[6]=(BYTE*)img->at(img,j-1,i+1);
                    if(j>=0&&i+1<=img->height)
                    ptr[7]=(BYTE*)img->at(img,j+0,i+1);
                    if(j+1<=img->width&&i+1<=img->height)
                    ptr[8]=(BYTE*)img->at(img,j+1,i+1);

                    P[i*img->width+j]=(double)((double)*ptr[2]+*ptr[5]*2+*ptr[8]-*ptr[0]-*ptr[3]*2-*ptr[6]);
                    Q[i*img->width+j]=(double)((double)*ptr[6]+*ptr[7]*2+*ptr[8]-*ptr[0]-*ptr[1]*2-*ptr[2]);    
                    Threa[i*img->width+j]=atan(Q[i*img->width+j]/P[i*img->width+j]);
                    ptr2=out->at(out,j,i);
                    *ptr2=sqrt(P[i*img->width+j]*P[i*img->width+j]+Q[i*img->width+j]*Q[i*img->width+j]);
                }
        }
        break;

        case LI_CANNY_ROBERTS:
         {
            for(int i=0;i<img->height-1;i++)
                for(int j=0;j<img->width-1;j++)
                {
                    BYTE* ptr[4];
                    BYTE* ptr2;
                    /**
                     * 2  3
                     * 0  1
                    */
                    ptr[0]=img->at(img,j,i);
                    ptr[1]=img->at(img,j+1,i);
                    ptr[2]=img->at(img,j,i+1);
                    ptr[3]=img->at(img,j+1,i+1);
                    ptr2=out->at(out,j,i);
                    *ptr2=abs(*ptr[2]-*ptr[1])+abs(*ptr[0]-*ptr[3]);
                    Threa[i*img->width+j]=atan(abs(*ptr[2]-*ptr[1])/abs(*ptr[0]-*ptr[3]));
                }         
         }
        break;

    case LI_CANNY_PREWITT:
          {
            for(int i=1;i<img->height-1;i++)
                for(int j=1;j<img->width-1;j++)
                {
                    BYTE* ptr[9];
                    BYTE* ptr2;
                    /**6  7  8
                     * 3  4  5
                     * 0  1  2
                     */
                    if(j-1>=0&&i-1>=0)
                    ptr[0]=(BYTE*)img->at(img,j-1,i-1);
                    if(j>=0&&i-1>=0)
                    ptr[1]=(BYTE*)img->at(img,j+0,i-1);
                    if(j+1<=img->width&&i-1>=0)
                    ptr[2]=(BYTE*)img->at(img,j+1,i-1);
                    if(j-1>=0&&i>=0)
                    ptr[3]=(BYTE*)img->at(img,j-1,i+0);
                    if(j>=0&&i>=0)
                    ptr[4]=(BYTE*)img->at(img,j+0,i+0);
                    if(j+1<=img->width&&i>=0)
                    ptr[5]=(BYTE*)img->at(img,j+1,i+0);
                    if(j-1>=0&&i+1<=img->height)
                    ptr[6]=(BYTE*)img->at(img,j-1,i+1);
                    if(j>=0&&i+1<=img->height)
                    ptr[7]=(BYTE*)img->at(img,j+0,i+1);
                    if(j+1<=img->width&&i+1<=img->height)
                    ptr[8]=(BYTE*)img->at(img,j+1,i+1);

                    P[i*img->width+j]=(double)((double)*ptr[2]+*ptr[5]+*ptr[8]-*ptr[0]-*ptr[3]-*ptr[6]);
                    Q[i*img->width+j]=(double)((double)*ptr[6]+*ptr[7]+*ptr[8]-*ptr[0]-*ptr[1]-*ptr[2]); 
                    Threa[i*img->width+j]=atan(Q[i*img->width+j]/P[i*img->width+j]);   
                    ptr2=out->at(out,j,i);
                    *ptr2=sqrt(P[i*img->width+j]*P[i*img->width+j]+Q[i*img->width+j]*Q[i*img->width+j]);
                }
        }      

        break;

    default:
        break;
    }

    #ifdef DEBUG
    Li_Save_Image("after_minus.bmp",out);
    #endif 

    /*非极大值抑制*/
    for(int j=1;j<out->height-1;j++)
        for(int i=1;i<out->width-1;i++)
        {
            double t=Threa[j*img->width+i];
            BYTE* ptr=out->at(out,i,j);
            double g=(double) *ptr;
            double g0, g1;
            if ((t >= -(3*M_PI/8)) && (t < -(M_PI/8)))
            {
                ptr=out->at(out,i-1,j-1);
                 g0=(double) *ptr;
                ptr=out->at(out,i+1,j+1);
                 g1=(double) *ptr;
            } 
            else if ((t >= -(M_PI/8)) && (t < M_PI/8))
            {
                ptr=out->at(out,i-1,j);
                 g0=(double) *ptr;
                ptr=out->at(out,i+1,j);
                 g1=(double) *ptr;
            }
            else if ((t >= M_PI/8) && (t < 3*M_PI/8))
            {
                ptr=out->at(out,i+1,j-1);
                 g0=(double) *ptr;
                ptr=out->at(out,i-1,j+1);
                 g1=(double) *ptr;
            }
            else
            {
                ptr=out->at(out,i,j-1);
                 g0=(double) *ptr;
                ptr=out->at(out,i,j+1);
                 g1=(double) *ptr;                
            }

            if (g <= g0 || g <= g1) {
                ptr=out->at(out,i,j);
                *ptr=0;
            }

        }

    /*阈值化操作*/
    #ifdef DEBUG
    Li_Save_Image("before_thre.bmp",out);
    #endif 
    Li_Image*out1=Li_Double_Threshold(out,min,max);
    #ifdef DEBUG
    Li_Save_Image("after_thre.bmp",out1);
    #endif 

    /*边缘链接*/
        for (int j = 1; j < out1->height-2; j++) 
        for (int i = 1; i < out1->width-2; i++) {
            BYTE* ptr=out1->at(out1,i,j);
            if(*ptr==255)
            {
                for (int m = -1; m < 1; m++) {
                    for (int n = -1; n < 1; n++) {
                    BYTE* temp=out1->at(out1,i+n,j+m);
                        if(*ptr!=0&&*ptr!=255)
                        *ptr=255;
                    }
                }             
            }
        }

        for (int j = 0; j < out1->height-1; j++) {
        for (int i = 0; i < out1->width-1; i++) {
            // 如果该点依旧是弱边缘点，及此点是孤立边缘点
             BYTE* ptr=out1->at(out1,i,j);
             if(*ptr!=255&&*ptr!=0)
             *ptr=0;
            }
        }
    Li_Destroy_Image(PP);
    Li_Destroy_Image(QQ);
    return out1;
}

#endif // !LI_CANNY_C

main.c

/*
 * @Descripttion: 
 * @version: 
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-10-26 19:35:49
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-12 10:01:13
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <malloc.h>
#include "bmp.h"
#include "cv.h"
#include "li_image.h"
#include "li_painter.h"
#include "li_image_proc.h"

int main()
{
     BYTE* ptr=NULL;
     Li_Image* out =Li_Load_Image("./picture/panal (1).jpg",LI_JPEG);
     Li_Image* bmp=Li_Convert_Image(out,LI_JPEG_2_BMP);
     Li_Image* gray=Li_Convert_Image(bmp,LI_BMP_888_2_LI_BMP_8);

     Li_Image* smooth=Li_Smooth(gray,Li_GAUSS);
     Li_Image* img= Li_Canny(smooth,LI_CANNY_PREWITT,30,150);
     Li_Save_Image("canny_mydefine.bmp",img);

     LILOG("over");
     return 0; 
}

（六）写在后面

因为LiteCV项目才刚刚写了一个开头，代码中有错误的地方还望指出。我已经将项目同步到了github，我会实时更新这个代码仓库。
项目github地址：
LiteCV

2021年7月6日2021年7月6日

【数字图像处理】图像形态学算法C语言实现（图像卷积，膨胀，腐蚀，开运算，闭运算，顶帽，黑帽，雕版，锐化）

@[TOC]

(一)图像卷积

1. 图像卷积

图像卷积是进行空间域滤波与梯度运算的基础。首先我们需要理解卷积的运算方式从而可以编程实现。

2. 数字信号处理中的卷积

卷积一词最开始出现在信号与线性系统中，信号与线性系统中讨论的就是信号经过一个线性系统以后发生的变化。由于现实情况中常常是一个信号前一时刻的输出影响着这一时刻的输出，所在一般利用系统的单位响应与系统的输入求卷积，以求得系统的输出信号（当然要求这个系统是线性时不变的）。
卷积的定义：
卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列x(n)和h(n)，则卷积的结果：

3 数字图像处理中的卷积

数字图像是一个二维的离散信号，对数字图像做卷积操作其实就是利用卷积核（卷积模板）在图像上滑动，将图像点上的像素灰度值与对应的卷积核上的数值相乘，然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值，并最终滑动完所有图像的过程。

图表 3
这张图可以清晰的表征出整个卷积过程中一次相乘后相加的结果：该图片选用3*3的卷积核，卷积核内共有九个数值，所以图片右上角公式中一共有九行，而每一行都是图像像素值与卷积核上数值相乘，最终结果-8代替了原图像中对应位置处的1。这样沿着图片一步长为1滑动，每一个滑动后都一次相乘再相加的工作，我们就可以得到最终的输出结果。除此之外，卷积核的选择有一些规则：
（1）卷积核的大小一般是奇数，这样的话它是按照中间的像素点中心对称的，所以卷积核一般都是3×3，5×5或者7×7。有中心了，也有了半径的称呼，例如5×5大小的核的半径就是2。
（2）卷积核所有的元素之和一般要等于1，这是为了原始图像的能量（亮度）守恒。其实也有卷积核元素相加不为1的情况，下面就会说到。
（3）如果滤波器矩阵所有元素之和大于1，那么滤波后的图像就会比原图像更亮，反之，如果小于1，那么得到的图像就会变暗。如果和为0，图像不会变黑，但也会非常暗。
（4）对于滤波后的结构，可能会出现负数或者大于255的数值。对这种情况，我们将他们直接截断到0和255之间即可。对于负数，也可以取绝对值。

（二）图像卷积实现各种形态学运算

腐蚀

极小值卷积，求局部极小值

膨胀

极大值卷积，求局部极大值

形态学梯度

开运算

闭运算

顶帽

黑帽

雕版

锐化

li_conv.c

/*
 * @Descripttion: 
 * @version: 
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-11-10 21:59:39
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-24 21:15:30
 */
#ifndef LI_CONV_C
#define LI_CONV_C



#include "cv.h"
#include "li_image_proc.h"
#include <stdio.h>


/**
 * @name: Li_GetKernel
 * @msg:  得到卷积核矩阵
 * @param {double* data 数据
 *         BYTE KernalKind 卷积核边长}
 * @return {Li_Kernel*}
 */
LI_API 
Li_Kernel* Li_GetKernel(double* data,BYTE KernalKind)
{
    Li_Kernel * kernel;
    kernel=(Li_Kernel*)li_malloc_arr(sizeof(Li_Kernel));
    kernel->arr=(double*)li_malloc_arr(KernalKind*KernalKind*sizeof(double));
    for(int i=0;i<KernalKind*KernalKind;i++)
    kernel->arr[i]=data[i];
    kernel->width=KernalKind;
    kernel->height=KernalKind;
    kernel->arrsize=KernalKind*KernalKind;
    return kernel;
}

/**
 * @name: Li_Convolute
 * @msg: 计算图像卷积
 * @param {Li_Image* img 卷积图像
 *         Li_Kernel* kernal 卷积核 }
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Convolute(Li_Image* img,Li_Kernel* kernal)
{
  if(img->imgdepth==LI_DEP_8U){
    if(kernal->width!=3) return NULL;
    BYTE* ptr[9]={0};
    BYTE* ptro;
    Li_Image* out=Li_Copy_Image(img);
    for(int i=0;i<img->height;i++)
        for(int j=0;j<img->width;j++)
        {
             BYTE sum=0;
             if(j-1>=0&&i-1>=0)
             ptr[0]=(BYTE*)img->at(img,j-1,i-1);
             if(j>=0&&i-1>=0)
             ptr[1]=(BYTE*)img->at(img,j+0,i-1);
             if(j+1<=img->width&&i-1>=0)
             ptr[2]=(BYTE*)img->at(img,j+1,i-1);
             if(j-1>=0&&i>=0)
             ptr[3]=(BYTE*)img->at(img,j-1,i+0);
             if(j>=0&&i>=0)
             ptr[4]=(BYTE*)img->at(img,j+0,i+0);
             if(j+1<=img->width&&i>=0)
             ptr[5]=(BYTE*)img->at(img,j+1,i+0);
             if(j-1>=0&&i+1<=img->height)
             ptr[6]=(BYTE*)img->at(img,j-1,i+1);
             if(j>=0&&i+1<=img->height)
             ptr[7]=(BYTE*)img->at(img,j+0,i+1);
             if(j+1<=img->width&&i+1<=img->height)
             ptr[8]=(BYTE*)img->at(img,j+1,i+1);
            for(int k=0;k<9;k++)
            {
                double* ptr2=(double*)(kernal->arr+k);
                if(ptr[k]!=NULL)
                {
                    sum+= (BYTE)(*ptr[k] * (*ptr2));
                }
                else 
                {
                    sum+=0;
                }
            }
            ptro=(BYTE*)out->at(out,j+0,i+0);
            *ptro=sum;
        }
        return out;
  }else if (img->imgdepth==LI_DEP_24U||img->imgdepth==LI_DEP_32U)
  {
     Li_Image* imgH[img->imgdepth+1];
     Li_Image* imgL[img->imgdepth+1];
     Li_Split(img,imgH);
     for(int i=0;i<img->imgdepth+1;i++)
     imgL[i]= Li_Convolute(imgH[i],kernal);     
     Li_Image* out2=Li_Combine(imgL,img->imgdepth);
     return out2;
  }
}


/**
 * @name: Li_Sharp
 * @msg:  图像锐化
 * @param {Li_Image* img}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Sharp(Li_Image* img)
{
    double data[9]={1,1,1,1,-7,1,1,1,1}; 
    if(img==NULL)return NULL;
    if(img->imgdepth==LI_DEP_8U){
        Li_Image* out;
        Li_Kernel* kernel;

        kernel=Li_GetKernel(data,3);
        out= Li_Convolute(img,kernel);
        return out;
    }else if (img->imgdepth==LI_DEP_24U||img->imgdepth==LI_DEP_32U)
    {
        Li_Image* imgH[img->imgdepth+1];
        Li_Image* imgL[img->imgdepth+1];
        Li_Split(img,imgH);
        for(int i=0;i<img->imgdepth+1;i++)  
        {
            imgL[i]=Li_Sharp(imgH[i]);
        }
        Li_Image* out2=Li_Combine(imgL,img->imgdepth);
        return out2;
    }
}

/**
 * @name: Li_Emboss
 * @msg:  图像雕版
 * @param {Li_Image* img}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Emboss(Li_Image* img)
{
    double data[9]={0,0,-1,0,-1,0,2,0,0}; 
    if(img==NULL)return NULL;
    if(img->imgdepth==LI_DEP_8U){
        Li_Image* out;
        Li_Kernel* kernel;

        kernel=Li_GetKernel(data,3);
        out= Li_Convolute(img,kernel);
        return out;
    }else if (img->imgdepth==LI_DEP_24U||img->imgdepth==LI_DEP_32U)
    {
        Li_Image* imgH[img->imgdepth+1];
        Li_Image* imgL[img->imgdepth+1];
        Li_Split(img,imgH);
        for(int i=0;i<img->imgdepth+1;i++)  
        {
            imgL[i]=Li_Emboss(imgH[i]);
        }
        Li_Image* out2=Li_Combine(imgL,img->imgdepth);
        return out2;
    }
}


/**
 * @name: Li_Erode
 * @msg: 图像腐蚀(局部最小)
 * @param {Li_Image* img}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Erode(Li_Image* img)
{
  if(img->imgdepth==LI_DEP_8U){
    BYTE kek=0;
    BYTE* ptr[9]={0};
    BYTE* ptro;
    Li_Image* out=Li_Copy_Image(img);
    for(int i=0;i<img->height;i++)
        for(int j=0;j<img->width;j++)
        {
             BYTE sum=0;
             for(int k=0;k<9;k++)
             ptr[k]=&kek;

             if(j-1>=0&&i-1>=0)
             ptr[0]=(BYTE*)img->at(img,j-1,i-1);
             if(j>=0&&i-1>=0)
             ptr[1]=(BYTE*)img->at(img,j+0,i-1);
             if(j+1<=img->width&&i-1>=0)
             ptr[2]=(BYTE*)img->at(img,j+1,i-1);
             if(j-1>=0&&i>=0)
             ptr[3]=(BYTE*)img->at(img,j-1,i+0);
             if(j>=0&&i>=0)
             ptr[4]=(BYTE*)img->at(img,j+0,i+0);
             if(j+1<=img->width&&i>=0)
             ptr[5]=(BYTE*)img->at(img,j+1,i+0);
             if(j-1>=0&&i+1<=img->height)
             ptr[6]=(BYTE*)img->at(img,j-1,i+1);
             if(j>=0&&i+1<=img->height)
             ptr[7]=(BYTE*)img->at(img,j+0,i+1);
             if(j+1<=img->width&&i+1<=img->height)
             ptr[8]=(BYTE*)img->at(img,j+1,i+1);

            BYTE temp[9];
            for(int k=0;k<9;k++)
            {
                if(ptr[k]!=NULL)
                {
                    temp[k]= (BYTE)(*ptr[k]);
                }
            }
            for(int m=0;m<9-1;m++)
                for(int n=0;n<9-m-1;n++)
                {
                    if(temp[m]>temp[m+1])
                    {
                        BYTE x=temp[m];
                        temp[m]=temp[n+1];
                        temp[n+1]=x;
                    }
                }
           ptro=(BYTE*)out->at(out,j+0,i+0);
           *ptro=temp[0];
        }
        return out;
  }else if (img->imgdepth==LI_DEP_24U||img->imgdepth==LI_DEP_32U)
  {
     Li_Image* imgH[img->imgdepth+1];
     Li_Image* imgL[img->imgdepth+1];
     Li_Split(img,imgH);
     for(int i=0;i<img->imgdepth+1;i++)
     imgL[i]= Li_Medeum(imgH[i]);     
     Li_Image* out2=Li_Combine(imgL,img->imgdepth);
     return out2;
  }
}


/**
 * @name: Li_Dilate
 * @msg: 图像膨胀(局部最小)
 * @param {Li_Image* img}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Dilate(Li_Image* img)
{
  if(img->imgdepth==LI_DEP_8U){
    BYTE kek=0;
    BYTE* ptr[9]={0};
    BYTE* ptro;
    Li_Image* out=Li_Copy_Image(img);
    for(int i=0;i<img->height;i++)
        for(int j=0;j<img->width;j++)
        {
             BYTE sum=0;
             for(int k=0;k<9;k++)
             ptr[k]=&kek;

             if(j-1>=0&&i-1>=0)
             ptr[0]=(BYTE*)img->at(img,j-1,i-1);
             if(j>=0&&i-1>=0)
             ptr[1]=(BYTE*)img->at(img,j+0,i-1);
             if(j+1<=img->width&&i-1>=0)
             ptr[2]=(BYTE*)img->at(img,j+1,i-1);
             if(j-1>=0&&i>=0)
             ptr[3]=(BYTE*)img->at(img,j-1,i+0);
             if(j>=0&&i>=0)
             ptr[4]=(BYTE*)img->at(img,j+0,i+0);
             if(j+1<=img->width&&i>=0)
             ptr[5]=(BYTE*)img->at(img,j+1,i+0);
             if(j-1>=0&&i+1<=img->height)
             ptr[6]=(BYTE*)img->at(img,j-1,i+1);
             if(j>=0&&i+1<=img->height)
             ptr[7]=(BYTE*)img->at(img,j+0,i+1);
             if(j+1<=img->width&&i+1<=img->height)
             ptr[8]=(BYTE*)img->at(img,j+1,i+1);

            BYTE temp[9];
            for(int k=0;k<9;k++)
            {
                if(ptr[k]!=NULL)
                {
                    temp[k]= (BYTE)(*ptr[k]);
                }
            }
            for(int m=0;m<9-1;m++)
                for(int n=0;n<9-m-1;n++)
                {
                    if(temp[m]>temp[m+1])
                    {
                        BYTE x=temp[m];
                        temp[m]=temp[n+1];
                        temp[n+1]=x;
                    }
                }
           ptro=(BYTE*)out->at(out,j+0,i+0);
           *ptro=temp[8];
        }
        return out;
  }else if (img->imgdepth==LI_DEP_24U||img->imgdepth==LI_DEP_32U)
  {
     Li_Image* imgH[img->imgdepth+1];
     Li_Image* imgL[img->imgdepth+1];
     Li_Split(img,imgH);
     for(int i=0;i<img->imgdepth+1;i++)
     imgL[i]= Li_Medeum(imgH[i]);     
     Li_Image* out2=Li_Combine(imgL,img->imgdepth);
     return out2;
  }
}

/**
 * @name: Li_Grandient
 * @msg: 形态学梯度
 * @param {Li_Image* img}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Grandient(Li_Image* img)
{
    Li_Image* erode=Li_Erode(img);
    Li_Image* dilate=Li_Dilate(img);
    Li_Image* minus=Li_Minus(dilate,erode);
    Li_Destroy_Image(erode);
    Li_Destroy_Image(dilate);
    return minus;
}

/**
 * @name: Li_Mod_Open
 * @msg: 形态学开运算
 * @param {Li_Image* img}
 * @return {Li_Image* }
 */
LI_API
Li_Image* Li_Mod_Open(Li_Image* img)
{
    Li_Image* dilate=Li_Dilate(img);//先膨胀
    Li_Image* erode=Li_Erode(dilate);//先腐蚀
    Li_Destroy_Image(dilate);
    return erode;
}

/**
 * @name: Li_Mod_Close
 * @msg: 形态学闭运算
 * @param {Li_Image* img}
 * @return {Li_Image* }
 */
LI_API
Li_Image* Li_Mod_Close(Li_Image* img)
{
    Li_Image* erode=Li_Erode(img);//先腐蚀
    Li_Image* dilate=Li_Dilate(erode);//先膨胀
    Li_Destroy_Image(erode);
    return dilate;
}

/**
 * @name: Li_TopHat
 * @msg: 图像顶帽运算
 * @param {Li_Image* img}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_TopHat(Li_Image* img)
{
    Li_Image* open=Li_Mod_Open(img);
    Li_Image* top=Li_Minus(img,open);
    Li_Destroy_Image(open);
    return top;
}

/**
 * @name: Li_BlackHat
 * @msg: 图像黑帽运算
 * @param {Li_Image* img}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_BlackHat(Li_Image* img)
{
    Li_Image* close=Li_Mod_Close(img);
    Li_Image* black=Li_Minus(img,close);
    Li_Destroy_Image(close);
    return black;
}

#endif // !LI_CONV_C

main.c

/*
 * @Descripttion: 图像卷积常见操作
 * @version: 
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-10-26 19:35:49
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-24 21:12:04
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <malloc.h>
#include "bmp.h"
#include "cv.h"
#include "li_image.h"
#include "li_painter.h"
#include "li_image_proc.h"

int main()
{
     BYTE* ptr=NULL;
     Li_Image* out =Li_Load_Image("./picture/whu_rgb888.bmp",LI_BMP_888);
     Li_Image* sharp=Li_Sharp(out);//图像锐化
     Li_Image* emboss=Li_Emboss(out);//雕版

     Li_Image* gray=Li_Convert_Image(out,LI_BMP_888_2_LI_BMP_8);
     Li_Image* bw  =Li_Threshold(gray,127);
     Li_Image* erode=Li_Erode(gray);//图像腐蚀
     Li_Image* dilate=Li_Dilate(gray);//图像膨胀
     Li_Image* add   =Li_Add(out,out);
     Li_Image* minus =Li_Minus(out,out);
     Li_Image* grand =Li_Grandient(gray);
     Li_Image* open  =Li_Mod_Open(gray);
     Li_Image* close =Li_Mod_Close(gray);
     Li_Image* top   =Li_TopHat(gray);
     Li_Image* black =Li_BlackHat(gray);

     Li_Image* noise =Li_Salt_Noise(out,1000);//椒盐噪声
     Li_Image* med =Li_Smooth(noise,Li_MEDIUM);//中值滤波
     Li_Image* conv=Li_Smooth(noise,Li_GAUSS);//高斯滤波
     Li_Image* ave=Li_Smooth(noise,Li_AVERAGE);//均值滤波

     Li_Save_Image("conv.bmp",conv);
     Li_Save_Image("sharp.bmp",sharp);
     Li_Save_Image("emboss.bmp",emboss);   
     Li_Save_Image("erode.bmp",erode); 
     Li_Save_Image("dilate.bmp",dilate);
     Li_Save_Image("gray.bmp",gray);
     Li_Save_Image("med.bmp",med); 
     Li_Save_Image("ave.bmp",ave); 
     Li_Save_Image("noise.bmp",noise);
     Li_Save_Image("add.bmp",add);
     Li_Save_Image("minus.bmp",minus);
     Li_Save_Image("grand.bmp",grand);
     Li_Save_Image("open.bmp",open);
     Li_Save_Image("close.bmp",close);
     Li_Save_Image("top.bmp",top);
     Li_Save_Image("black.bmp",black);
     LILOG("over");
     return 0; 
}

(三)效果展示

原图

腐蚀

膨胀

形态学梯度

开运算

闭运算

顶帽

黑帽

雕版

锐化

（四）写在后面

因为LiteCV项目才刚刚写了一个开头，代码中有错误的地方还望指出。我已经将项目同步到了github，我会实时更新这个代码仓库。
项目github地址：
LiteCV

2021年7月6日2021年7月6日

【数字图像处理】图像滤波C语言实现（中值，均值，高斯）

@[TOC]

（一）均值滤波

用其像素点周围像素的平均值代替元像素值，在滤除噪声的同时也会滤掉图像的边缘信息。

通过编程实现一个3X3的均值滤波器（example/conv/conv.c），滤波效果如下：

图表 4 均值滤波1

图表 5 均值滤波2
分析：均值滤波算法简单能很快的对图像进行平滑处理, 也就是能将由于屏幕显示的分辨率不高的图像出现的锯齿边缘平滑, 均值滤波的缺点是由于对对图像锯齿边缘进行平滑处理而导致图像趋于模糊。

（二）高斯滤波

• 像均值滤波，是简单的取平均值，模板系数都是1。而图像上的像素实际上是坐标离散但是值却连续的，因为越靠近的点关系越密切，越远离的点关系越疏远。因此，加权平均更合理，距离越近的点权重越大，距离越远的点权重越小。
• 既然是依据距离来加权平均，那么很容易想到高斯函数

如图所示：

从高斯函数来看，离原点距离越近，得到的权重越高，越远离原点，得到的权重越小。
上边是一维的高斯函数，当中心点为原地时，x的均值μ=0，此时

由于图像是二维矩阵，则采用二维高斯函数：

有了这个函数就可以计算滤波模板中每个点的权重了
我采用如下高斯卷积核实现了高斯模糊（example/conv/conv.c）：

得到如下滤波结果：

图表 6 高斯滤波1

图表 7 高斯滤波2
分析：高斯滤波对于高斯噪声处理效果特别好, 由于高斯噪声是由中心点开始呈现模糊, 具有一定的模糊半径, 但一般不知道模糊半径和边缘方向。而高斯滤波很好地处理了这一问题, 因为二维高斯函数具有旋转对称性, 所以使用高斯滤波处理图像时不会出现偏向任意一方的情况, 而且邻域内的像素的权重是随离中心点的距离单调递减的, 所以使用高斯滤波处理图像时不会对边缘的影响过大, 不会像均值滤波那样因为过度的平滑处理而导致图像边缘模糊而导致图像失真。但是高斯滤波的缺点也很突出, 高斯滤波这种图像处理方式基本上只能运用于高斯噪声。总的来说, 高斯滤波能很好地滤除高斯噪声, 而且对图像的平滑更好, 不会造成图像的大幅度模糊, 对边缘的处理效果也较好, 缺点是基本只能运用于高斯噪声, 对椒盐噪声等其它噪声很难达到好的滤波效果。

（三）中值滤波

不同于以上两种滤波方式，中值滤波用测试像素周围邻域像素集中的中值代替原像素。中值滤波去除椒盐噪声和斑块噪声时，效果非常明显。

图表 8 中值滤波1

图表 9 中值滤波2
　分析：中值滤波的优点有很多, 首先中值滤波操作方式简单, 其次, 根据中值滤波的算法可知中值滤波可以很好地保护图像的边缘信息不被破坏, 再者中值滤波选择合适的点来替代图像中的污染点, 而保护图像的大部分内容, 中值滤波尤其适用于椒盐噪声的处理, 因为椒盐噪声的图像内有干净点和污染点, 通过处理污染点就被合适的点替换, 所以中值滤波可以很好地滤除椒盐噪声。但中值滤波也有缺点, 一般来说图像中比较明亮和比较暗的区域都通过中值滤波滤除, 但是较大区域的噪声一般会原封不动的保存下来。所以, 经分析中值滤波对于区域较大的噪声的滤除效果不好, 对于点状噪声的滤除效果最好尤其是椒盐噪声。

（四）选择滤波算法

综上我们发现高斯滤波对于图像边缘信息的保存会更加完整，所以我们选择了高斯滤波算法。

（五）代码实现

li_smooth.c

/*
 * @Descripttion: 
 * @version: 
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-11-10 22:01:04
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-10 22:44:07
 */
#ifndef LI_SMOOTH_C
#define LI_SMOOTH_C



#include "cv.h"
#include "li_image_proc.h"
#include <stdio.h>

/**
 * @name: Li_Medeum
 * @msg: 图像中值滤波
 * @param {Li_Image* img}
 * @return {Li_Image*}
 */
Li_Image* Li_Medeum(Li_Image* img)
{
  if(img->imgdepth==LI_DEP_8U){
    BYTE kek=0;
    BYTE* ptr[9]={0};
    BYTE* ptro;
    Li_Image* out=Li_Copy_Image(img);
    for(int i=0;i<img->height;i++)
        for(int j=0;j<img->width;j++)
        {
             BYTE sum=0;
             for(int k=0;k<9;k++)
             ptr[k]=&kek;

             if(j-1>=0&&i-1>=0)
             ptr[0]=(BYTE*)img->at(img,j-1,i-1);
             if(j>=0&&i-1>=0)
             ptr[1]=(BYTE*)img->at(img,j+0,i-1);
             if(j+1<=img->width&&i-1>=0)
             ptr[2]=(BYTE*)img->at(img,j+1,i-1);
             if(j-1>=0&&i>=0)
             ptr[3]=(BYTE*)img->at(img,j-1,i+0);
             if(j>=0&&i>=0)
             ptr[4]=(BYTE*)img->at(img,j+0,i+0);
             if(j+1<=img->width&&i>=0)
             ptr[5]=(BYTE*)img->at(img,j+1,i+0);
             if(j-1>=0&&i+1<=img->height)
             ptr[6]=(BYTE*)img->at(img,j-1,i+1);
             if(j>=0&&i+1<=img->height)
             ptr[7]=(BYTE*)img->at(img,j+0,i+1);
             if(j+1<=img->width&&i+1<=img->height)
             ptr[8]=(BYTE*)img->at(img,j+1,i+1);

            BYTE temp[9];
            for(int k=0;k<9;k++)
            {

                if(ptr[k]!=NULL)
                {
                    temp[k]= (BYTE)(*ptr[k]);
                }
            }
            for(int m=0;m<9-1;m++)
                for(int n=0;n<9-m-1;n++)
                {
                    if(temp[m]>temp[m+1])
                    {
                        BYTE x=temp[m];
                        temp[m]=temp[n+1];
                        temp[n+1]=x;
                    }
                }
           ptro=(BYTE*)out->at(out,j+0,i+0);
           *ptro=temp[4];
        }
        return out;
  }else if (img->imgdepth==LI_DEP_24U||img->imgdepth==LI_DEP_32U)
  {
     Li_Image* imgH[img->imgdepth+1];
     Li_Image* imgL[img->imgdepth+1];
     Li_Split(img,imgH);
     for(int i=0;i<img->imgdepth+1;i++)
     imgL[i]= Li_Medeum(imgH[i]);     
     Li_Image* out2=Li_Combine(imgL,img->imgdepth);
     return out2;
  }
}

/**
 * @name: Li_Smooth
 * @msg: 计算图像滤波
 * @param {Li_Image* img 原图像
 *         BYTE smoothtype( Li_GAUSS,   //高斯滤波
                            Li_AVERAGE, //均值滤波
                            Li_MEDIUM,  //中值滤波)}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Smooth(Li_Image* img,BYTE smoothtype)
{
    if(img==NULL)return NULL;
    Li_Image* out;
    Li_Kernel* kernel;
    double data1[9]={1.0/9,1.0/9,1.0/9,1.0/9,1.0/9,1.0/9,1.0/9,1.0/9,1.0/9};
    double data2[9]={1.0/16,2.0/16,1.0/16,2.0/16,4.0/16,2.0/16,1.0/16,2.0/16,1.0/16};
    switch (smoothtype)
    {
    case Li_AVERAGE:

        kernel=Li_GetKernel(data1,3);
        out= Li_Convolute(img,kernel);
        break;
    case Li_GAUSS:

        kernel=Li_GetKernel(data2,3);
        out= Li_Convolute(img,kernel);
        break;

    case Li_MEDIUM:
        out=Li_Medeum(img);
        break;

    default:
        break;
    }
    return out;

}


/**
 * @name: Li_Salt_Noise
 * @msg:  图像椒盐噪声
 * @param {Li_Image* img
 *         LONG num 噪点数量}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Salt_Noise(Li_Image* img,LONG num)
{
    Li_Image* out=Li_Copy_Image(img);
    for(int i=0;i<num;i++){
    LONG x=(LONG)(rand()%img->width);
    LONG y=(LONG)(rand()%img->height);
    BYTE * ptr= out->at(out,x,y);
    int r = rand()%2;
        if(r)
        {
        for(int j=0;j<=img->imgdepth;j++)
            *ptr++=0;
        }
        else
        {
        for(int j=0;j<=img->imgdepth;j++)
            *ptr++=0xFF;
        }  
    }
    return out; 
}


#endif // !LI_SMOOTH_C

main.c

/*
 * @Descripttion: 图像卷积常见操作
 * @version: 
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-10-26 19:35:49
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-24 21:12:04
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <malloc.h>
#include "bmp.h"
#include "cv.h"
#include "li_image.h"
#include "li_painter.h"
#include "li_image_proc.h"

int main()
{
     BYTE* ptr=NULL;
     Li_Image* out =Li_Load_Image("./picture/whu_rgb888.bmp",LI_BMP_888);

     Li_Image* noise =Li_Salt_Noise(out,1000);//椒盐噪声
     Li_Image* med =Li_Smooth(noise,Li_MEDIUM);//中值滤波
     Li_Image* conv=Li_Smooth(noise,Li_GAUSS);//高斯滤波
     Li_Image* ave=Li_Smooth(noise,Li_AVERAGE);//均值滤波

     Li_Save_Image("conv.bmp",conv);
     Li_Save_Image("med.bmp",med); 
     Li_Save_Image("ave.bmp",ave); 
     Li_Save_Image("noise.bmp",noise);

     LILOG("over");
     return 0; 
}

（六）写在后面

因为LiteCV项目才刚刚写了一个开头，代码中有错误的地方还望指出。我已经将项目同步到了github，我会实时更新这个代码仓库。
项目github地址：
LiteCV

2021年7月6日2021年7月6日

【数字图像处理】指针式仪表示数读取C语言实现

@[TOC]
经过一个月的努力终于将LiteCV体系架构初步完成。
以下是开发说明：

LiteCV 使用说明

（一）写在前面

或许你会存在这样的需求，对于一张图片你根本无需对其作出太过复杂的处理，但是你有没有，
办法可以很方便的读取一张图片，无论采用什么外部库你都需要经过一些很麻烦，甚至可以说
是并不友好的一些事情。而因为采用了外部的库，而当那些库并不简单的时候，对于底层的
一些东西就不再变得那么可控了。那么有没有办法可以实现图片的简单读取，同时也可以实现
对底层的完全控制呢。

在大概在一年多以前我就已经在尝试着做一些与图像处理有关的工作了，当时完成了底层的IO
读写，与一些简单的例如灰度增强与仿射变换等工作，但是非常遗憾的是由于当时对于底层数
据架构的处理并不是非常完善，导致后面的工作变得越来越难以进行，所以在最近，我又尝试
重新进行底层架构。目前的整个体系架构可以参考doc\Litecv体系架构.km文件。在这个基础
上我又写了一篇可以通过这个架构进行表盘指针读数的文章，参考doc\应用Litecv的表盘读数
论文.docx。对于现在的体系架构我总体上还是比较满意的。目前已经可以支持常见的文件类型
（BMP，JPEG，PNG）的读写。遗憾的是，并没有做任何与UI有关的工作，导致无法实时显示任
何图片，但这并不重要，对于外部库更少的依赖就意味着你可以更方便的进行移植与编译。

（二）简单的测试一下吧

（1）Windows下的测试

如果你用的是windows电脑，那么就很简单了，你可以双击win_build下的任何一个可执行文件，
这些程序实现了一些常用的功能例如图片读取与显示，对于图片进行画笔操作。图像滤波卷积，
边缘检测等等，在这个时候，当前文件夹下多出的文件就是这个程序生成的文件。

（2）Linux下的测试

和上面一样，进入linux_build文件夹./XXX 运行相应的程序

（3）arm

请转到下面的编译

（三）如何快捷的编译代码

（1）首先我们来看一下我们需要编译哪些文件

Core文件夹中，我们只需要编译li_image.c ,为啥嘞，
Core文件夹下的其他文件都已经被我include到li_image.c
文件中了，所以编译会很简单。

对于头文件请在编译选项中引入以下头文件目录：
Litecv\inc\Core

Imgproc中的文件可以选择不编译，如果你只想要实现一些最
简单的IO读取功能的话。如果需要编译的话那么只要编译
li_image_proc.c文件即可。

对于头文件请在编译选项中引入以下头文件目录：
Litecv\inc\Imgproc

（2）怎么编译呢

对于使用GNU套件的人来说，那就很简单了，因为我们使用了
Cmake的管理工具，但是如果你用的是其他的编译器的话也不
要紧，反正只有两个文件，编译应该问题不大。就是将前面两
个文件一起编译即可。

（I）windows下的编译

（一）按照我写的脚本编译

1）你需要先下载以下两个软件

MinGW下载地址

Cmake下载地址

（2）修改编译文件
就是CMakeLists.txt文件如下

cmake_minimum_required(VERSION 3.2)
project(LICV)
include_directories (Litecv/inc/Core)
include_directories (Litecv/inc/Imgproc)
aux_source_directory(./ DIR_MAIN)
set(LICV_MAIN ${DIR_MAIN})

add_compile_options(-std=c99)

aux_source_directory(./example/basicio DIR_EXP01)
set(LICV_EXP01 ${DIR_EXP01})
aux_source_directory(./example/painter DIR_EXP02)
set(LICV_EXP02 ${DIR_EXP02})
aux_source_directory(./example/conv   DIR_EXP04)
set(LICV_EXP04 ${DIR_EXP04})
aux_source_directory(./example/canny   DIR_EXP05)
set(LICV_EXP05 ${DIR_EXP05})

set(ARM OFF)

if(ARM)
aux_source_directory(./example/arm9 DIR_EXP03)
set(LICV_EXP03 ${DIR_EXP03})

else()
if (CMAKE_HOST_WIN32)
    set(WINDOWS ON)
elseif (CMAKE_HOST_APPLE)
    set(MACOS   ON)
elseif (CMAKE_HOST_UNIX)
    set(LINUX   ON)
endif ()
endif()


set(USE_JPEG   ON)
set(USE_PNG    ON)
add_subdirectory(Litecv)


add_executable(${PROJECT_NAME} ${LICV_MAIN})
target_link_libraries(${PROJECT_NAME} licvcore)
target_link_libraries(${PROJECT_NAME} licvimgproc)

add_executable(IO ${LICV_EXP01})
target_link_libraries(IO licvcore)

add_executable(Painter ${LICV_EXP02})
target_link_libraries(Painter licvcore)

add_executable(smooth ${LICV_EXP04})
target_link_libraries(smooth licvcore)
target_link_libraries(smooth licvimgproc)

add_executable(canny ${LICV_EXP05})
target_link_libraries(canny licvcore)
target_link_libraries(canny licvimgproc)


if(ARM)
add_executable(display ${LICV_EXP03})
target_link_libraries(display licvcore)
endif(ARM)

就是将

set(USE_JPEG   ON)
set(USE_PNG    ON)

改成

set(USE_JPEG   OFF)
set(USE_PNG    OFF)

再将inc/Core/cv.h文件中的

//是否支持JPEG与PNG
#define EN_JPEG 1
#define EN_PNG  1

改为

//是否支持JPEG与PNG
#define EN_JPEG 0
#define EN_PNG  0

这样就可以编译了

进入win_build，当然也可以自己新建一个文件
运行

 cmake.exe ../ -G "MinGW Makefiles"
 mingw32-make.exe

(二)gcc直接编译的方法

Makefile我就不写了

gcc -c .\li_image.c -I../inc/Core -o li_image.o

ar -r .\li_image.a .\li_image.o

gcc -c .\li_image_proc.c -I..\inc\Core\  -I..\inc\Imgproc\ -o li_image_proc.o

ar -r .\li_image_proc.a .\li_image_proc.o

gcc .\main.c  .\Litecv\Core\li_image.a .\Litecv\Imgproc\li_image_proc.a  -I.\Litecv\inc\Core\  -I.\Litecv\inc\Imgproc\ -o Licv

（3）不想用jpeg，png图片的可以不看了

这里使用的是从网上下载的MinGw版本，将路径C:MinGW\bin加到”环境变量”→”系统变量”→”Path”
命令行输入：
gcc -v
可看到gcc版本为：gcc version 8.1.0 (rev2, Built by MinGW-builds project)

MSYS

下载地址：http://www.mingw.org/wiki/MSYS
当前版本：1.0.11
一路安装下去即可

zlib

下载地址：http://www.zlib.net/
当前版本：1.2.11
命令行输入：

cp win32\makefile.gcc makefile.gcc
mingw32-make -f makefile.gcc

生成libz.a文件

libpng

下载地址：http://www.libpng.org/pub/png/libpng.html
当前版本：1.6.37
打开scripts/makefile.gcc设置zlib路径：

ZLIBINC = ../zlib-1.2.11
ZLIBLIB = ../zlib-1.2.11

拷贝scripts/pnglibconf.h.prebuilt到源码目录，改名为pnglibconf.h
命令行输入：

cp scripts\makefile.gcc makefile.gcc
mingw32-make -f makefile.gcc

生成libpng.a文件

libjpeg

下载地址：http://www.ijg.org/
当前版本：9
打开MSYS (rxvt)，输入：

cd jpeg-9
./configure
make

若是出现以下错误：

jcapimin.c:127:1: error: conflicting types for ‘jpeg_suppress_tables’
jpeg_suppress_tables (j_compress_ptr cinfo, boolean suppress)

打开jconfig.h，增加以下定义：

define HAVE_PROTOTYPES 1

重新输入：

make

上面的库编完以后修改：

Litecv\CMakeLists.txt文件
cmake_minimum_required(VERSION 3.2)
include_directories(
    inc/Core
    inc/Imgproc
)
FILE(GLOB DIR_SRCS  "Core/li_image.c")
FILE(GLOB PROC_SRCS "Imgproc/li_image_proc.c")

SET(LICV_CORE ${DIR_SRCS})
SET(LICV_PROC ${PROC_SRCS})

#根据实际情况修改静态库的绝对路径
#linux中不需要指定库的头文件目录
if(LINUX)
    if(USE_JPEG)
    include_directories(/home/swann/LiteCV/Litecv/3rd/linux_3rd_lib/jpeg_linux_install/include)
    #include_directories(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/linux_3rd_lib/jpeg_linux_install/include)
    #使用编译器自带的jpeg库
    link_libraries(/home/swann/LiteCV/Litecv/3rd/linux_3rd_lib/jpeg_linux_install/lib/libjpeg.a)
    #link_libraries(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/linux_3rd_lib/jpeg_linux_install/lib/libjpeg.a)
    #link_libraries(libjpeg.a )
    endif(USE_JPEG)

    if(USE_PNG)

    include_directories(/home/swann/LiteCV/Litecv/3rd/linux_3rd_lib/png_linux_install/include)
    link_libraries(/home/swann/LiteCV/Litecv/3rd/linux_3rd_lib/png_linux_install/lib/libpng16.a)
    link_libraries(/home/swann/LiteCV/Litecv/3rd/linux_3rd_lib/zlib_linux_install/lib/libz.a)

    #include_directories(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/arm_3rd_build/png_arm_install/include)
    #link_libraries(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/linux_3rd_lib/png_linux_install/lib/libpng.a)
    #link_libraries(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/linux_3rd_lib/zlib_linux_install/lib/libz.a )
    link_libraries(  m)
    endif(USE_PNG)

elseif(WINDOWS)
    if(USE_JPEG)
    include_directories(E:/LiteCV/Litecv/3rd/win_3rd_lib/jpeg_win_install/include)
    link_libraries(E:/LiteCV/Litecv/3rd/win_3rd_lib/jpeg_win_install/lib/libjpeg.a )
    endif(USE_JPEG)
    if(USE_PNG)
    include_directories( E:/LiteCV/Litecv/3rd/win_3rd_lib/png_win_install/include)
    link_libraries(  E:/LiteCV/Litecv/3rd/win_3rd_lib/png_win_install/lib/libpng.a)
    link_libraries(  E:/LiteCV/Litecv/3rd/win_3rd_lib/zlib_win_install/lib/libz.a )
    link_libraries(  m)
    endif(USE_PNG)

elseif(ARM)
    Message(ARM)
    if(USE_JPEG)
    include_directories(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/arm_3rd_build/jpeg_arm_install/include)
    #使用编译器自带的jpeg库
    link_libraries(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/arm_3rd_build/jpeg_arm_install/lib/libjpeg.a)
    endif(USE_JPEG)

    if(USE_PNG)
    include_directories(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/arm_3rd_build/png_arm_install/include)
    link_libraries(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/arm_3rd_build/png_arm_install/lib/libpng.a)
    link_libraries(/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/arm_3rd_build/zlib_arm_install/lib/libz.a)
    link_libraries(  m)
    endif(USE_PNG)
endif()
add_library(licvcore   STATIC  ${LICV_CORE})
add_library(licvimgproc STATIC  ${LICV_PROC})

把目录改一下。

（II）Linux下的编译与arm交叉编译

和windows基本一样，新建一个文件

cmake ..

make 即可

如果是交叉编译可以在cmake-gui中修改编译器

#### libjpeg编译：

下载libjpeg源码：http://www.ijg.org/ 下载jpegsrc.v9a.tar.gz
解压源码,命令：tar -zxvf jpegsrc.v9a, 源码文件夹为jpeg-9a
运行命令：./configure –prefix=jpeg-9a/release –enable-shared=no
在jpeg-9a下查找Makefile文件并打开，查找CFLAGS，在CFLAGS = -g -02 后面添加 -fPIC
运行命令：make
运行命令：make install
最终静态库文件安装在jpeg-9a/release/lib下

libPng编译：

编译libPng首先需要编译zlib，过程如下：

下载zlib源码zlib-1.2.11.tar.gz
解压zlib源码到zlib-1.2.11
运行命令：./configure –static 静态编译
在zlib-1.2.11下查找Makefile文件并打开，查找CFLAGS 并在该行最后加上 -fPIC
运行命令：make
运行命令：make install

下面编译libpng

下载源码libpng-1.6.37.tar.gz
解压到libpng-1.6.37
运行命令：./configure –prefix=libpng-1.6.37/release –enable-shared=no
在libpng-1.6.13下查找Makefile文件并打开，查找CFLAGS并在该行最后加上 -fPIC
运行命令：make
运行命令：make install

最后将所有的库文件归拢一下就OK了

(3) 交叉编译

./configure –prefix=/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/src/libpng-1.6.37/png_arm_install –host=arm-linux CC=arm-none-linux-gnueabi-gcc CFLAGS=-I/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/src/zlib-1.2.11/zlib_arm_install/include LDFLAGS=-L/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/src/zlib-1.2.11/zlib_arm_install/lib –prefix=/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/src/libpng-1.6.37/png_arm_install

//change makefile
DEFAULT_INCLUDES = -I.
DEFAULT_INCLUDES +=-I/home/swann/IMX_283A/Qt/App/LiteCV/Litecv/3rd/src/zlib-1.2.11/zlib_arm_install/include

基于已经写好的体系架构实现指针读数

建立图像底层架构实现完成对于图像的基本处理方法。
对于指针式仪表图像的预处理技术的研究：对于多种图像滤波算法进行比较；对于Canny边缘检测的多种梯度算子的效果进行比较同时选择双阈值法进行图像分割。
仪表刻度识别：采用圆检测算法，在检测出圆的感兴趣区域中进行霍夫直线检测，再将检测出的直线角度，通过刻度线的分布特征进行读数识别。

/*
 * @Descripttion: 
 * @version: 
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-10-26 19:35:49
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-12 11:13:48
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <malloc.h>
#include "bmp.h"
#include "cv.h"
#include "li_image.h"
#include "li_painter.h"
#include "li_image_proc.h"
#include "math.h"

#define MINDIS 0.0   //最小刻度值对应数值
#define MINTHE 50.0  //最小的刻度对应角度
#define MAXDIS 0.6   //最大刻度值对应数值
#define MAXTHE MINTHE+265 //最大的刻度对应角度


int main()
{
     LiLine l;
     LiCircle c;
     Li_Image* out,*bmp,*gray,*smooth,*canny,*roi ;
     char* picname="./picture/panal (";
     char outfile[20];
     char infile[20];
     for(int i=0;i<11;i++){
          sprintf(infile,"%s%d%s",picname,i+1,").jpg");
          sprintf(outfile,"%s%d%s","out",i+1,".bmp");

          LILOG("NEXT PICTURE");
          out=Li_Load_Image(infile,LI_JPEG);
          bmp=Li_Convert_Image(out,LI_JPEG_2_BMP);
          gray=Li_Convert_Image(bmp,LI_BMP_888_2_LI_BMP_8);
          smooth=Li_Smooth(gray,Li_GAUSS);

          canny= Li_Canny(smooth,LI_CANNY_SOBEL,50,128);

          LONG range[]={170,180,100,120};
          Li_Hough_Circle(canny,&c,120,130,range);

          c.r=c.r- c.r%8;
          LONG startx=c.x-c.r ;
          LONG starty=c.y-c.r;
          LONG endx=c.x+c.r ,endy=c.y+c.r;
          roi=Li_Get_Roi(canny,(startx)>0?(startx):0,(starty)>0?(starty):0,(endx)<canny->width?(endx):canny->width,(endy)<canny->height?(endy):canny->height);
          Li_Hough_Line(roi,&l,130,250);

          Li_Image* res=Li_Get_Roi(bmp,(startx)>0?(startx):0,(starty)>0?(starty):0,(endx)<bmp->width?(endx):bmp->width,(endy)<bmp->height?(endy):bmp->height);
          Li_Line_P(res,0xFF0000,l.thera,l.r);
          Li_Circle(res,0x00FF00,(res->width-2)/2,(res->height-2)/2,c.r);

          double read;
          char text[30];
          if(l.thera<=90)
          read=(180-l.thera-MINTHE)*((MAXDIS-MINDIS)/(MAXTHE-MINTHE));
          else
          read=(360-l.thera-MINTHE)*((MAXDIS-MINDIS)/(MAXTHE-MINTHE));

          printf("%d",l.thera);
          sprintf(text,"read num: %lf",read);
          Li_String(res,0x0000FF,40,40,150,30,text,12);
          Li_Save_Image("./smooth.bmp",smooth);
          Li_Save_Image("./canny_sobel.bmp",canny);
          Li_Save_Image("./roi.bmp",roi);
          Li_Save_Image(outfile,res);
     }
     LILOG("over");
     return 0; 
}

第一步滤波

第二步梯度化与边缘检测

第三步检测圆后获取感兴趣区域

第四步直线检测与读数

2021年7月6日2021年7月6日

【数字图像处理】编码解码jpeg和png图片（C语言实现）

摘要：在本篇文章中本人将简单阐述图片编码的原理与实现方法。同时
通过 windows平台下 mingw编译的libjpeg，libpng, zlib 第三方库，然后实现两种图片的编码与解码。

（一）写在前面

前一段时间本人一直在进行Opencv有关的学习，可是在学完了一堆又一堆的函数之后，发现自己对于图像处理的知识其实本质上还是什么都不会。我相信真正图像处理一定不是仅仅调用几个函数就可以了事的，一些东西如果不自己敲一遍恐怕永远也无法懂得其真正的原理。所以我打算从最底层自己敲出一个轻量级的图像处理库出来。可能一开始我的代码并不可靠效率可能也赶不上那些开源库的效率，但是我坚信这个轮子造的一定是有意义的。
截止目前为之，这个图像处理的库已经可以支持jpeg,png,bmp三种图片格式的编码和解码。同时对于一些图片的常见几何变化，灰度变换，颜色识别等功能都已经分别进行了实现。而且截止目前仍然具有跨平台的特性。稍作修改便可以运行在
X86_LINUX,ARN_LINUX,STM32
等平台上面。
下面的计划就是进一步的扩展界面显示的功能。比较凄惨的是找了半天也没有找到合适又简单的C语言跨平台图像库，这个再自己写又好像不太现实，所以决定开始导入QT作为图像显示的载体。

我目前已经将这个项目开源于github
LiteCV

（二）基础知识

（1）图像的压缩与解码

（2）常用的图像压缩方法

1.哈夫曼编码

2.香农范诺编码

（2）静止图像压缩编码标准（JPEG）

看了那么多PPT个人感觉还是没有完全搞明白JPEG是个什么东西，感觉主要就是往频域做了一步变化，然后就是一顿骚操作，看起开似乎要自己写是不可能了，确实有些复杂。那就只能调用库文件了，好在这几个库都是开源的跨平台的时候直接编译一下就好了。

关于库的编译我就不细说了，不像opencv编译的时候那么多坑，装一个cmake就可以轻松编译成功了。要是实在懒得去编译可以到我的gihub代码仓库里面找一下，是有那几个第三方库的源码和库文件的。

（三）软件实现

jpeg.c

/*
 * @Descripttion: 向licvcore 提供jpegJ读写接口
 * @version: V 2.0
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-11-10 22:18:19
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-10 22:40:47
 */
#ifndef JPEG_C
#define JPEG_C


#ifdef USE_JPEG

#include "jconfig.h"
#include "jmorecfg.h"
#include <jpeglib.h>
#include <setjmp.h>
#include "cv.h"

/**
 * @name: 
 * @msg: 将RGB数据编码并写JPG图片
 * @param
 *        char *filepath        图片路径
 *        JSAMPLE *image_buffer RGB数据指针
 *        int quality           图片质量
 *        int image_width      图片高度
 *        int image_height       图片宽度
 * @return 0 (right) or -1(something wrong)
 */
BYTE Write_Jpeg(BYTE *filepath,JSAMPLE *image_buffer, LONG quality,LONG image_width,LONG image_height)
{
  struct jpeg_compress_struct cinfo;
  struct jpeg_error_mgr jerr;
  FILE *outfile;          
  JSAMPROW row_pointer[1];
  int row_stride;

  cinfo.err = jpeg_std_error(&jerr);
  /* Now we can initialize the JPEG compression object. */
  jpeg_create_compress(&cinfo);

  if ((outfile = fopen(filepath, "wb")) == NULL) {
    LILOG("can't open");
    return -1;
  }
  jpeg_stdio_dest(&cinfo, outfile);
  cinfo.image_width = image_width;    
  cinfo.image_height = image_height;
  cinfo.input_components = 3;
  cinfo.in_color_space = JCS_RGB;
  jpeg_set_defaults(&cinfo);
  jpeg_set_quality(&cinfo, quality, TRUE);
  jpeg_start_compress(&cinfo, TRUE);
  row_stride = (image_width * 3 + 3) & ~3;
  int i=0,j=0;
  for(i=0;i<image_height;i++)
    for(j=0;j<image_width;j++)
    {
      BYTE temp=image_buffer[3*image_width*i+3*j];
      image_buffer[3*image_width*i+3*j]=image_buffer[3*image_width*i+3*j+2];
      image_buffer[3*image_width*i+3*j+2]=temp;
    }
  while (cinfo.next_scanline < cinfo.image_height) {
    row_pointer[0] = &image_buffer[(cinfo.image_height-cinfo.next_scanline) * row_stride];
    (void)jpeg_write_scanlines(&cinfo, row_pointer, 1);
  }
  jpeg_finish_compress(&cinfo);
  fclose(outfile);
  jpeg_destroy_compress(&cinfo);
}

struct my_error_mgr {
  struct jpeg_error_mgr pub; 

  jmp_buf setjmp_buffer; 
};

typedef struct my_error_mgr *my_error_ptr;

METHODDEF(void)
my_error_exit(j_common_ptr cinfo)
{
  my_error_ptr myerr = (my_error_ptr)cinfo->err;
  (*cinfo->err->output_message) (cinfo);
  longjmp(myerr->setjmp_buffer, 1);
}


/**
 * @name: Read_Jpeg
 * @msg: 读取一个JPG图片
 * @param char* filepath 图片路径
 *        LONG* wdith    返回图片的宽度
 *        LONG* height   返回图片的高度
 * @return 数据指针
 */
BYTE* Read_Jpeg(char* filepath,LONG* width,LONG* height)
{
  BYTE *imgData;
  struct jpeg_decompress_struct cinfo;
  struct my_error_mgr jerr;
  FILE *infile;
  JSAMPARRAY buffer;
  int row_stride; 
  if ((infile = fopen(filepath, "rb")) == NULL) {
    LILOG("can't open");
  }
  cinfo.err = jpeg_std_error(&jerr.pub);
  jerr.pub.error_exit = my_error_exit;
  if (setjmp(jerr.setjmp_buffer)) {
    LILOG("ERROR");
    jpeg_destroy_decompress(&cinfo);
    fclose(infile);
  }
  jpeg_create_decompress(&cinfo);
  jpeg_stdio_src(&cinfo, infile);
  jpeg_read_header(&cinfo, TRUE);
  jpeg_start_decompress(&cinfo);
  row_stride = (cinfo.output_width * 3 );
  imgData=(BYTE*)malloc(cinfo.output_height*cinfo.output_width*3);
  buffer =malloc(row_stride*1);
  while (cinfo.output_scanline < cinfo.output_height) {
     jpeg_read_scanlines(&cinfo, (JSAMPARRAY)&buffer,1);
      char *p = (char*)buffer;
      for (int x = 0; x <cinfo.output_width; x++)
      {
          *(imgData+(cinfo.output_height-cinfo.output_scanline)*row_stride+3*x+2) = *p++;
          *(imgData+(cinfo.output_height-cinfo.output_scanline)*row_stride+3*x+1) = *p++;
          *(imgData+(cinfo.output_height-cinfo.output_scanline)*row_stride+3*x+0) = *p++; 
      }
  }
  *width=cinfo.output_width;
  *height=cinfo.output_height;
  free(buffer);
  (void)jpeg_finish_decompress(&cinfo);
  jpeg_destroy_decompress(&cinfo);
  fclose(infile);
  return imgData;
}

#endif //USE_JPEG


#endif // !JPE_CG

png.c

/*
 * @Descripttion: 向licvcore 提供png读写接口
 * @version: V 2.0
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-11-10 22:18:19
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-10 22:41:48
 */

#ifndef LI_PNG_C
#define LI_PNG_C


#ifdef USE_PNG

#include "png.h"
#include "cv.h"
#define PNG_BYTES_TO_CHECK    8
#define HAVE_ALPHA            1
#define NOT_HAVE_ALPHA        0

typedef struct _pic_data pic_data;
struct _pic_data {
    int width, height;  //长宽
    int bit_depth;      //位深度
    int alpha_flag;     //是否有透明通道
    unsigned char *rgba;//实际rgb数据
};

BYTE check_is_png(FILE **fp, const char *filename) //检查是否png文件
{
    char checkheader[PNG_BYTES_TO_CHECK]; //查询是否png头
    *fp = fopen(filename, "rb");
    if (*fp == NULL) {
        LILOG("open failed ...1\n");
        return -1;
    }
    if (fread(checkheader, 1, PNG_BYTES_TO_CHECK, *fp) != PNG_BYTES_TO_CHECK) //读取png文件长度错误直接退出
        return 0;
    return png_sig_cmp(checkheader, 0, PNG_BYTES_TO_CHECK); //0正确, 非0错误
}

/**
 * @name: Read_Png
 * @msg: 读取一个png图片
 * @param char* filepath  图片路径
 *        LONG* wdith     返回图片的宽度
 *        LONG* height    返回图片的高度
 *        BYTE* withalpha 是否带有alpha通道
 * @return 数据指针 注：一定返回一个24位的数据指针
 */
BYTE* Read_Png(BYTE *filename,LONG* width,LONG* height) //取出png文件中的rgb数据
{
  pic_data *out =(pic_data*)malloc(sizeof(pic_data));
    png_structp png_ptr; //png文件句柄
    png_infop   info_ptr;//png图像信息句柄
    int ret;
    FILE *fp;
    if (check_is_png(&fp, filename) != 0) {
        LILOG("file is not png ...\n");
        return NULL;
    }
    png_ptr  = png_create_read_struct(PNG_LIBPNG_VER_STRING, NULL, NULL, NULL); 
    info_ptr = png_create_info_struct(png_ptr);
    setjmp(png_jmpbuf(png_ptr));
    rewind(fp);
    png_init_io(png_ptr, fp);
    png_read_png(png_ptr, info_ptr, PNG_TRANSFORM_EXPAND, 0); //读取文件信息
    int channels, color_type; 
    channels    = png_get_channels(png_ptr, info_ptr); //通道数量
    color_type  = png_get_color_type(png_ptr, info_ptr);//颜色类型
    out->bit_depth = png_get_bit_depth(png_ptr, info_ptr);//位深度 
    out->width   = png_get_image_width(png_ptr, info_ptr);//宽
    out->height  = png_get_image_height(png_ptr, info_ptr);//高
    *width=out->width;
  *height=out->height;
    if(color_type == PNG_COLOR_TYPE_PALETTE)
        png_set_palette_to_rgb(png_ptr);//要求转换索引颜色到RGB
    if(color_type == PNG_COLOR_TYPE_GRAY && out->bit_depth < 8)
        png_set_expand_gray_1_2_4_to_8(png_ptr);//要求位深度强制8bit
    if(out->bit_depth == 16)
        png_set_strip_16(png_ptr);//要求位深度强制8bit
    if(png_get_valid(png_ptr,info_ptr,PNG_INFO_tRNS))
        png_set_tRNS_to_alpha(png_ptr);
    if(color_type == PNG_COLOR_TYPE_GRAY || color_type == PNG_COLOR_TYPE_GRAY_ALPHA)
        png_set_gray_to_rgb(png_ptr);//灰度必须转换成RG

    int i, j, k;
    int size, pos = 0;
    int temp;

    png_bytepp row_pointers; //实际存储rgb数据的buf
    row_pointers = png_get_rows(png_ptr, info_ptr); //也可以分别每一行获取png_get_rowbytes();
    size = out->width * out->height; //申请内存先计算空间
    if (channels == 4 || color_type == PNG_COLOR_TYPE_RGB_ALPHA) { //判断是24位还是32位
        out->alpha_flag = HAVE_ALPHA; //记录是否有透明通道
        size *= (sizeof(unsigned char) * 4); //size = out->width * out->height * channel
        out->rgba = (png_bytep)malloc(size);
        if (NULL == out->rgba) {
            LILOG("malloc rgba faile ...\n");
            png_destroy_read_struct(&png_ptr, &info_ptr, 0);
            fclose(fp);
            return NULL;
        }
        //从row_pointers里读出实际的rgb数据
        for (i = out->height-1; i >0; i --) {
            for (j = 0; j < 4 * out->width; j += 4) {
                out->rgba[pos++] = row_pointers[i][j+2];
                out->rgba[pos++] = row_pointers[i][j+1];
                out->rgba[pos++] = row_pointers[i][j+0];
        out->rgba[pos++] = row_pointers[i][j+3];
            }
        }
    } 
  else if (channels == 3 || color_type == PNG_COLOR_TYPE_RGB) { //判断颜色深度是24位还是32位
    out->alpha_flag = NOT_HAVE_ALPHA;
        size *= (sizeof(unsigned char) * 4);
        out->rgba = (png_bytep)malloc(size);
        if (NULL == out->rgba) {
            LILOG("malloc rgba faile ...\n");
            png_destroy_read_struct(&png_ptr, &info_ptr, 0);
            fclose(fp);
            return NULL;
        }
        //从row_pointers里读出实际的rgb数据
        temp = (3 * out->width);
        for (i = 0; i < out->height; i ++) {
            for (j = 0; j < temp; j += 3) {
                out->rgba[pos++] = row_pointers[i][j+2];
                out->rgba[pos++] = row_pointers[i][j+1];
                out->rgba[pos++] = row_pointers[i][j+0];
        pos++;
            }
        }
    } else return NULL; 
    //6:销毁内存
    png_destroy_read_struct(&png_ptr, &info_ptr, 0);
    fclose(fp);
    //此时， 我们的out->rgba里面已经存储有实际的rgb数据了
    //处理完成以后free(out->rgba)
    return out->rgba;
}


/**
 * @name: Write_Png
 * @msg:  写一个png图片
 * @param BYTE*  png_file_name 文件名称
 *        BYTE*  pixels        数据指针
 *        int    width         图像宽度
 *        int    height        图像高度
 *        int    withalpha     是否带有alpha通道
 * @return 0成功 -1失败
 */
BYTE Write_Png(BYTE* png_file_name, BYTE*  pixels , LONG width, LONG height)
{
  pic_data *out=malloc(sizeof(pic_data));
  out->bit_depth=8;
  out->rgba=pixels;
  out->alpha_flag=HAVE_ALPHA;
  out->height=height;
  out->width=width;

    png_structp png_ptr;
    png_infop   info_ptr;
    png_byte color_type;
    png_bytep * row_pointers;
    FILE *fp = fopen(png_file_name, "wb");
    if (NULL == fp) {
        LILOG("open failed ...2");
        return -1;
    }
    //1: 初始化libpng结构体  
    png_ptr = png_create_write_struct(PNG_LIBPNG_VER_STRING, 0, 0, 0);
    if (!png_ptr) {
        LILOG("png_create_write_struct failed ...");
        return -1;
    }
    //2: 初始化png_infop结构体 ， 
    //此结构体包含了图像的各种信息如尺寸，像素位深, 颜色类型等等
    info_ptr = png_create_info_struct(png_ptr);
    if (!info_ptr) {
        LILOG("png_create_info_struct failed ...\n");
        return -1;
    }
    //3: 设置错误返回点
    if (setjmp(png_jmpbuf(png_ptr))) {
        LILOG("error during init_io ...\n");
        return -1;
    }
    //4:绑定文件IO到Png结构体
    png_init_io(png_ptr, fp);
    if (setjmp(png_jmpbuf(png_ptr))) {
        LILOG("error during init_io ...\n");
        return -1;
    }
    if (out->alpha_flag == HAVE_ALPHA) color_type = PNG_COLOR_TYPE_RGB_ALPHA;
    else color_type = PNG_COLOR_TYPE_RGB;
    //5：设置以及写入头部信息到Png文件
    png_set_IHDR(png_ptr, info_ptr, out->width, out->height, out->bit_depth,
    color_type, PNG_INTERLACE_NONE, PNG_COMPRESSION_TYPE_BASE, PNG_FILTER_TYPE_BASE);
    png_write_info(png_ptr, info_ptr);
    if (setjmp(png_jmpbuf(png_ptr))) {
        LILOG("error during init_io ...\n");
        return -1;
    }
    int channels, temp;
    int i, j, pos = 0;
    if (out->alpha_flag == HAVE_ALPHA) {
        channels = 4;
        temp = (4 * out->width);
    } else {
        channels = 3;
        temp = (3 * out->width);
    }
    row_pointers = (png_bytep*)malloc(out->height * sizeof(png_bytep));
    for (i = out->height-1; i >=0; i--) {
        row_pointers[i] = (png_bytep)malloc(temp* sizeof(unsigned char));
        for (j = 0; j < temp; j += channels) {
            if (channels == 4) {
                row_pointers[i][j+2] = out->rgba[pos++];
                row_pointers[i][j+1] = out->rgba[pos++];
                row_pointers[i][j+0] = out->rgba[pos++];
                row_pointers[i][j+3] = out->rgba[pos++];
            } else {
                row_pointers[i][j+2] = out->rgba[pos++];
                row_pointers[i][j+1] = out->rgba[pos++];
                row_pointers[i][j+0] = out->rgba[pos++];
            }
        }
    }
    png_write_image(png_ptr, (png_bytepp)row_pointers);
    if (setjmp(png_jmpbuf(png_ptr))) {
        return -1;
    }
    //7: 写入尾部信息
    png_write_end(png_ptr, NULL);
    //8:释放内存 ,销毁png结构体
    for (i = 0; i < out->height; i ++)
        free(row_pointers[i]);
    free(row_pointers);
    png_destroy_write_struct(&png_ptr, &info_ptr);
    fclose(fp);
    return 0;
}


#endif //USE_PNG


#endif // !LI_PAINTER_C

(四)效果展示

/*
 * @Descripttion: 底层图片IO测试
 * @version: V 2.0
 * @Author: Yueyang
 * @email: 1700695611@qq.com
 * @Date: 2020-10-26 19:35:49
 * @LastEditors: Yueyang
 * @LastEditTime: 2020-11-04 15:50:21
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <malloc.h>
#include "bmp.h"
#include "cv.h"
#include "li_image.h"
int main()
{
     //加载保存销毁图片
     Li_Image* out=Li_Load_Image("./picture/whu_rgb888.bmp",LI_BMP_888);
     Li_Save_Image("./picture/1.bmp",out);
     Li_Destroy_Image(out);

     Li_Image* out3=Li_Load_Image("./picture/whu_gray.bmp",LI_BMP_8);  
     Li_Save_Image("./picture/2.bmp",out3);   
     Li_Destroy_Image(out3);

     Li_Image* out4=Li_Load_Image("./picture/whu_rgba.bmp",LI_BMP_32);  
     Li_Save_Image("./picture/3.bmp",out4);  
     Li_Destroy_Image(out4);

     Li_Image* out1=Li_Load_Image("./picture/whu_png.png",LI_PNG);
     Li_Save_Image("./picture/1.png",out1);
     Li_Destroy_Image(out1);

     Li_Image* out2=Li_Load_Image("./picture/whu_jpg.jpg",LI_JPEG);
     Li_Save_Image("./picture/1.jpg",out2);
     Li_Destroy_Image(out2);


     //创建图片并操作像素
     BYTE* ptr=NULL;
     Li_Image* out7 =Li_Create_Image(300,300,LI_DEP_24U,LI_BMP_888);
     ptr=out7->at(out7,10,10);
     if(ptr!=NULL){
          memset(ptr,0xFF,1);
          memset(ptr+1,0,1);  
          memset(ptr+2,0,1);            
     }
     Li_Save_Image("./picture/1.bmp",out3);
     Li_Destroy_Image(out7);

     Li_Image* out8 =Li_Load_Image("./picture/whu_jpg.jpg",LI_JPEG);
     ptr=out8->at(out8,10,10);
     if(ptr!=NULL){
          memset(ptr,0xFF,1);
          memset(ptr+1,0,1);  
          memset(ptr+2,0,1);
     }
     Li_Save_Image("./picture/2.jpg",out8);
     Li_Destroy_Image(out8);

     Li_Image* out5 =Li_Load_Image("./picture/whu_png.png",LI_PNG);
     ptr=out5->at(out5,10,10);
     if(ptr!=NULL){
          memset(ptr,0xFF,1);
          memset(ptr+1,0,1);  
          memset(ptr+2,0,1);
     }
     Li_Save_Image("./picture/2.png",out5);

     Li_Image* out6=Li_Copy_Image(out5);
     Li_Save_Image("./picture/3.png",out6);


     LILOG("over");
     return 0; 
}

左边是png图片读取为BMP同时显示，右边是JPEG经过高倍压缩再解压后的图片。

2021年7月6日2021年7月6日

【数字图像处理】图像的灰度变换和直方图均衡化处理

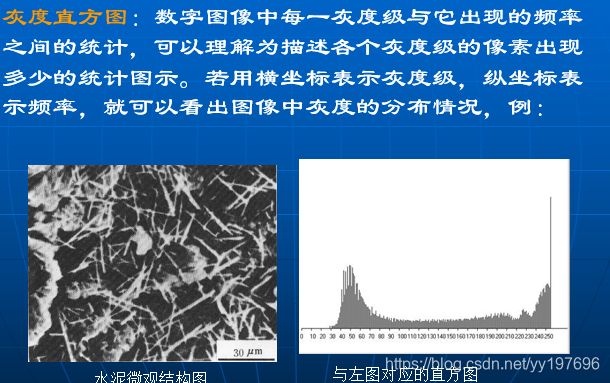
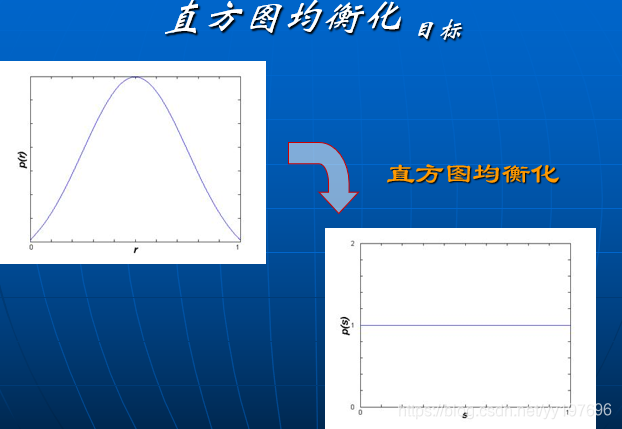
摘要：在本篇文章中我将先对于灰度变换的一些基础的知识进行陈述。在那之后我将基于先前已经完成的基于图像处理的基础代码实现图像的灰度变换。为了可以绘制一幅直方图，我不得不在从底层实现一些基础的画笔工具，随后基于前面的灰度变换，我可以绘制出一幅图像的直方图。基于直方图可以对于图像的一些基础的特征进行分析。接着实现了一个可以进行直方图均衡化处理的函数，实现图像加强的目标。最后基于一种特殊的情况分析直方图均衡化的局限性。

（一）写在前面

我目前已经将这个项目开源于github
LiteCV

（二）基础知识

（1）灰度变换

对于数字图像处理而言，一般包含着空间域处理和变换域处理两种形式。空间域处理方法主要是直接以图像中的像素操作为基础，它主要分为灰度变换和空间滤波两类。灰度变换是在图像的单个像素上操作，主要以对比度和阈值处理为目的。空间域处理可由下式表示：

                  g(x,y)=T[f(x,y)]

其中f(x,y)是输入图像，g(x,y)是处理后的图像，T是在点(x,y)的领域上定义的关于f的一种算子。

为了保证经过灰度变换后的输出图像在整体的外貌上，或者更准确地说在形态学上，与输入图像保持一致，灰度变换函数必须是严格单调递增函数。在图像处理中，灰度变换主要应用于图像的对比度改善。在灰度变换中，最为常用的三类基本函数为线性函数（反转和恒等变换）、对数函数（对数和反对数变换）以及幂律函数（n次幂和n次根变换）。恒等函数是最一般的情况，其输出图像灰度等于输入图像灰度的变换。

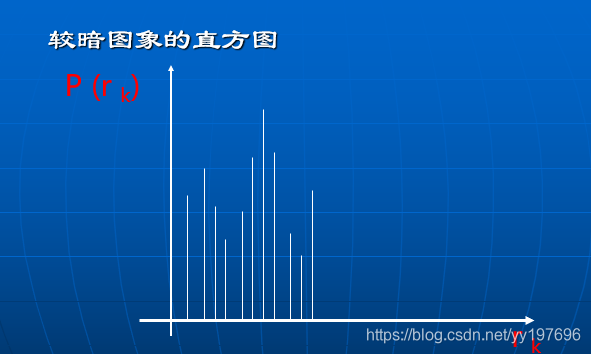
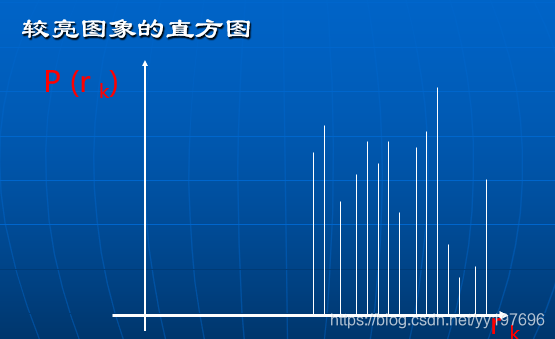
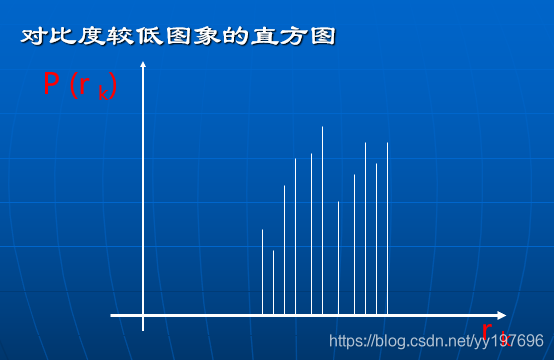
（2）灰度直方图

(3)基于灰度直方图的图像增强

（三）软件实现

（1）因为涉及到直方图绘制需要先，实现一个画笔工具箱

LI_API
void Li_Point(Li_Image* mat,LONG color,LONG x,LONG y)
{
    if(x>=0&&x<mat->width&&y>0&&y<mat->height)
    {
        BYTE* inaddr;
        inaddr=mat->at(mat,x,y);
        *inaddr=(u8)((color&0x00FF0000)>>16);//B
        *(inaddr+1)=(u8)((color&0x0000FF00)>>8);//G
        *(inaddr+2)=(u8)(color&0x000000FF);//R
    }
}


LI_API
void Li_Line(Li_Image* mat,LONG color,LONG x1, LONG y1, LONG x2, LONG y2)
{
    u16 t;
    int xerr=0,yerr=0,delta_x,delta_y,distance;
    int incx,incy,uRow,uCol;
    delta_x=x2-x1; //计算坐标增量
    delta_y=y2-y1;
    uRow=x1;
    uCol=y1;
    if(delta_x>0)incx=1; //设置单步方向
    else if(delta_x==0)incx=0;//垂直线
    else {incx=-1;delta_x=-delta_x;}
    if(delta_y>0)incy=1;
    else if(delta_y==0)incy=0;//水平线
    else{incy=-1;delta_y=-delta_y;}
    if( delta_x>delta_y)distance=delta_x; //选取基本增量坐标轴
    else distance=delta_y;
    for(t=0;t<=distance+1;t++ )//画线输出
    {
        Li_Point(mat,color,uRow, uCol);
        xerr+=delta_x ;
        yerr+=delta_y ;
        if(xerr>distance)
        {
            xerr-=distance;
            uRow+=incx;
        }
        if(yerr>distance)
        {
            yerr-=distance;
            uCol+=incy;
        }
    }
}

LI_API 
void Li_Line_H(Li_Image* mat,LONG color,LONG x, LONG length)
{
    Li_Line(mat,color,x,0,x,length);
}

LI_API
void Li_Line_P(Li_Image* mat,LONG color,LONG threa, LONG R)
{
    float fRate = (float)(PI/180);
    for(int x=1;x<mat->width;x++)
     {
          LONG y=(R-x*cos(threa*fRate))/sin(threa* fRate);
          LONG y1=(R-(x-1)*cos(threa*fRate))/sin(threa* fRate);
          if(y<mat->height&&y1<mat->height)
          Li_Line(mat,color, x,  y,  x-1,  y1);
     }
}


LI_API
void Li_Circle(Li_Image* mat ,LONG color,LONG x0,LONG y0,LONG r)
{
    int a,b;
    int di;
    a=0;b=r;
    di=3-(r<<1);             //判断下个点位置的标志
    while(a<=b)
    {
        Li_Point(mat,color,x0+a, y0-b);
        Li_Point(mat,color,x0+b, y0-a);
        Li_Point(mat,color,x0+b, y0+a);
        Li_Point(mat,color,x0+a, y0+b);
        Li_Point(mat,color,x0-a, y0+b);
        Li_Point(mat,color,x0-b, y0+a);
        Li_Point(mat,color,x0-a, y0-b);
        Li_Point(mat,color,x0-b, y0-a);
        a++;
        //使用Bresenham算法画圆
        if(di<0)di +=4*a+6;
        else
        {
            di+=10+4*(a-b);
            b--;
        }
    }
}

LI_API
void Li_Char(Li_Image* mat,LONG color,LONG x,LONG y,BYTE num,BYTE size)
{
    u8 temp,t1,t;
    y=mat->height-y;
    u16 y0=y;
    u8 csize=(size/8+((size%8)?1:0))*(size/2);        //得到字体一个字符对应点阵集所占的字节数
    num=num-' ';//得到偏移后的值（ASCII字库是从空格开始取模，所以-' '就是对应字符的字库）
    for(t=0;t<csize;t++)
    {
        if(size==LI_FONT_12)temp=asc2_1206[num][t];         //调用1206字体
        else if(size==LI_FONT_16)temp=asc2_1608[num][t];    //调用1608字体
        else if(size==LI_FONT_24)temp=asc2_2412[num][t];    //调用2412字体
        else if(size==LI_FONT_32)temp=asc2_3216[num][t];    //调用3216字体
        else return;                                //没有的字库
        for(t1=0;t1<8;t1++)
        {
            if(temp&0x80)Li_Point(mat,color,x,mat->height-y);
            temp<<=1;
            y++;
            if(y>=mat->width)return;        //超区域了
            if((y-y0)==size)
            {
                y=y0;
                x++;
                if(x>=mat->height)return;    //超区域了
                break;
            }
        }
    }
}


LI_API
void Li_String(Li_Image* mat,LONG color,LONG x,LONG y,LONG width,LONG height,BYTE*p,BYTE size)
{
    u8 x0=x;
    width+=x;
    height+=y;
    while((*p<='~')&&(*p>=' '))//判断是不是非法字符!
    {
        if(x>=width){x=x0;y+=size;}
        if(y>=height)break;//退出
        Li_Char(mat,color,x, y, *p ,size);
        x+=size/2;
        p++;
    }
}

上面的文件涉及到一个字体文件因为文件太大这里就不具体给出，大家可以从github中下载

（2）将彩色图片灰度化

这里直接采用了256阶的灰度值，在获取灰度图片的同时返回一个数组记录整个图片的灰度值

/**
 *  Y = 0.299 * R + 0.587 * G + 0.114 * B;
    Y=D+E+F;
    D=0.299*R;
    E=0.587*G;
    F=0.114*B;
*/
static short int YMap[3][256]={
{0,0,0,0,1,1,1,2,2,2,2,3,3,3,4,4,4,5,5,5,5,6,6,6,7,7,7,8,8,8,8,9,9,9,10,10,10,11,11,11,11,12,12,12,13,13,13,14,14,14,14,15,15,15,16,16,16,17,17,17,17,18,18,18,19,19,19,20,20,20,20,21,21,21,22,22,22,23,23,23,23,24,24,24,25,25,25,25,26,26,26,27,27,27,28,28,28,28,29,29,29,30,30,30,31,31,31,31,32,32,32,33,33,33,34,34,34,34,35,35,35,36,36,36,37,37,37,37,38,38,38,39,39,39,40,40,40,40,41,41,41,42,42,42,43,43,43,43,44,44,44,45,45,45,46,46,46,46,47,47,47,48,48,48,49,49,49,49,50,50,50,51,51,51,51,52,52,52,53,53,53,54,54,54,54,55,55,55,56,56,56,57,57,57,57,58,58,58,59,59,59,60,60,60,60,61,61,61,62,62,62,63,63,63,63,64,64,64,65,65,65,66,66,66,66,67,67,67,68,68,68,69,69,69,69,70,70,70,71,71,71,72,72,72,72,73,73,73,74,74,74,75,75,75,75,76},
{0,0,1,1,2,2,3,4,4,5,5,6,7,7,8,8,9,9,10,11,11,12,12,13,14,14,15,15,16,17,17,18,18,19,19,20,21,21,22,22,23,24,24,25,25,26,26,27,28,28,29,29,30,31,31,32,32,33,34,34,35,35,36,36,37,38,38,39,39,40,41,41,42,42,43,44,44,45,45,46,46,47,48,48,49,49,50,51,51,52,52,53,53,54,55,55,56,56,57,58,58,59,59,60,61,61,62,62,63,63,64,65,65,66,66,67,68,68,69,69,70,71,71,72,72,73,73,74,75,75,76,76,77,78,78,79,79,80,80,81,82,82,83,83,84,85,85,86,86,87,88,88,89,89,90,90,91,92,92,93,93,94,95,95,96,96,97,98,98,99,99,100,100,101,102,102,103,103,104,105,105,106,106,107,107,108,109,109,110,110,111,112,112,113,113,114,115,115,116,116,117,117,118,119,119,120,120,121,122,122,123,123,124,125,125,126,126,127,127,128,129,129,130,130,131,132,132,133,133,134,134,135,136,136,137,137,138,139,139,140,140,141,142,142,143,143,144,144,145,146,146,147,147,148,149,149},
{0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,6,6,6,6,6,6,6,6,6,7,7,7,7,7,7,7,7,7,8,8,8,8,8,8,8,8,9,9,9,9,9,9,9,9,9,10,10,10,10,10,10,10,10,10,11,11,11,11,11,11,11,11,11,12,12,12,12,12,12,12,12,12,13,13,13,13,13,13,13,13,14,14,14,14,14,14,14,14,14,15,15,15,15,15,15,15,15,15,16,16,16,16,16,16,16,16,16,17,17,17,17,17,17,17,17,18,18,18,18,18,18,18,18,18,19,19,19,19,19,19,19,19,19,20,20,20,20,20,20,20,20,20,21,21,21,21,21,21,21,21,22,22,22,22,22,22,22,22,22,23,23,23,23,23,23,23,23,23,24,24,24,24,24,24,24,24,24,25,25,25,25,25,25,25,25,25,26,26,26,26,26,26,26,26,27,27,27,27,27,27,27,27,27,28,28,28,28,28,28,28,28,28,29}
};

/**
 *  U = - 0.1687 R - 0.3313 G + 0.5 B + 128
    Y=D+E+F;
    D=- 0.1687 R;
    E=- 0.3313 G;
    F=  0.5 B;
*/
static short int UMap[3][256]={
{0,-1,-1,-1,-1,-1,-2,-2,-2,-2,-2,-2,-3,-3,-3,-3,-3,-3,-4,-4,-4,-4,-4,-4,-5,-5,-5,-5,-5,-5,-6,-6,-6,-6,-6,-6,-7,-7,-7,-7,-7,-7,-8,-8,-8,-8,-8,-8,-9,-9,-9,-9,-9,-9,-10,-10,-10,-10,-10,-10,-11,-11,-11,-11,-11,-11,-12,-12,-12,-12,-12,-12,-13,-13,-13,-13,-13,-13,-14,-14,-14,-14,-14,-15,-15,-15,-15,-15,-15,-16,-16,-16,-16,-16,-16,-17,-17,-17,-17,-17,-17,-18,-18,-18,-18,-18,-18,-19,-19,-19,-19,-19,-19,-20,-20,-20,-20,-20,-20,-21,-21,-21,-21,-21,-21,-22,-22,-22,-22,-22,-22,-23,-23,-23,-23,-23,-23,-24,-24,-24,-24,-24,-24,-25,-25,-25,-25,-25,-25,-26,-26,-26,-26,-26,-26,-27,-27,-27,-27,-27,-27,-28,-28,-28,-28,-28,-29,-29,-29,-29,-29,-29,-30,-30,-30,-30,-30,-30,-31,-31,-31,-31,-31,-31,-32,-32,-32,-32,-32,-32,-33,-33,-33,-33,-33,-33,-34,-34,-34,-34,-34,-34,-35,-35,-35,-35,-35,-35,-36,-36,-36,-36,-36,-36,-37,-37,-37,-37,-37,-37,-38,-38,-38,-38,-38,-38,-39,-39,-39,-39,-39,-39,-40,-40,-40,-40,-40,-40,-41,-41,-41,-41,-41,-41,-42,-42,-42,-42,-42,-43,-43,-43,-43,-43,-43,-44},
{0,-1,-1,-1,-2,-2,-2,-3,-3,-3,-4,-4,-4,-5,-5,-5,-6,-6,-6,-7,-7,-7,-8,-8,-8,-9,-9,-9,-10,-10,-10,-11,-11,-11,-12,-12,-12,-13,-13,-13,-14,-14,-14,-15,-15,-15,-16,-16,-16,-17,-17,-17,-18,-18,-18,-19,-19,-19,-20,-20,-20,-21,-21,-21,-22,-22,-22,-23,-23,-23,-24,-24,-24,-25,-25,-25,-26,-26,-26,-27,-27,-27,-28,-28,-28,-29,-29,-29,-30,-30,-30,-31,-31,-31,-32,-32,-32,-33,-33,-33,-34,-34,-34,-35,-35,-35,-36,-36,-36,-37,-37,-37,-38,-38,-38,-39,-39,-39,-40,-40,-40,-41,-41,-41,-42,-42,-42,-43,-43,-43,-44,-44,-44,-45,-45,-45,-46,-46,-46,-47,-47,-47,-48,-48,-48,-49,-49,-49,-50,-50,-50,-51,-51,-51,-52,-52,-52,-53,-53,-53,-54,-54,-54,-55,-55,-55,-55,-56,-56,-56,-57,-57,-57,-58,-58,-58,-59,-59,-59,-60,-60,-60,-61,-61,-61,-62,-62,-62,-63,-63,-63,-64,-64,-64,-65,-65,-65,-66,-66,-66,-67,-67,-67,-68,-68,-68,-69,-69,-69,-70,-70,-70,-71,-71,-71,-72,-72,-72,-73,-73,-73,-74,-74,-74,-75,-75,-75,-76,-76,-76,-77,-77,-77,-78,-78,-78,-79,-79,-79,-80,-80,-80,-81,-81,-81,-82,-82,-82,-83,-83,-83,-84,-84,-84,-85,-85},
{0,0,1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10,11,11,12,12,13,13,14,14,15,15,16,16,17,17,18,18,19,19,20,20,21,21,22,22,23,23,24,24,25,25,26,26,27,27,28,28,29,29,30,30,31,31,32,32,33,33,34,34,35,35,36,36,37,37,38,38,39,39,40,40,41,41,42,42,43,43,44,44,45,45,46,46,47,47,48,48,49,49,50,50,51,51,52,52,53,53,54,54,55,55,56,56,57,57,58,58,59,59,60,60,61,61,62,62,63,63,64,64,65,65,66,66,67,67,68,68,69,69,70,70,71,71,72,72,73,73,74,74,75,75,76,76,77,77,78,78,79,79,80,80,81,81,82,82,83,83,84,84,85,85,86,86,87,87,88,88,89,89,90,90,91,91,92,92,93,93,94,94,95,95,96,96,97,97,98,98,99,99,100,100,101,101,102,102,103,103,104,104,105,105,106,106,107,107,108,108,109,109,110,110,111,111,112,112,113,113,114,114,115,115,116,116,117,117,118,118,119,119,120,120,121,121,122,122,123,123,124,124,125,125,126,126,127,127}
};
/**
 *  V = 0.5 R - 0.4187 G - 0.0813 B + 128
    Y=D+E+F;
    D=  0.5 R;
    E=- 0.4187 G ;
    F=- 0.0813 B;
*/
static short int VMap[3][256]={
{0,0,1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10,11,11,12,12,13,13,14,14,15,15,16,16,17,17,18,18,19,19,20,20,21,21,22,22,23,23,24,24,25,25,26,26,27,27,28,28,29,29,30,30,31,31,32,32,33,33,34,34,35,35,36,36,37,37,38,38,39,39,40,40,41,41,42,42,43,43,44,44,45,45,46,46,47,47,48,48,49,49,50,50,51,51,52,52,53,53,54,54,55,55,56,56,57,57,58,58,59,59,60,60,61,61,62,62,63,63,64,64,65,65,66,66,67,67,68,68,69,69,70,70,71,71,72,72,73,73,74,74,75,75,76,76,77,77,78,78,79,79,80,80,81,81,82,82,83,83,84,84,85,85,86,86,87,87,88,88,89,89,90,90,91,91,92,92,93,93,94,94,95,95,96,96,97,97,98,98,99,99,100,100,101,101,102,102,103,103,104,104,105,105,106,106,107,107,108,108,109,109,110,110,111,111,112,112,113,113,114,114,115,115,116,116,117,117,118,118,119,119,120,120,121,121,122,122,123,123,124,124,125,125,126,126,127,127},
{0,-1,-1,-2,-2,-3,-3,-3,-4,-4,-5,-5,-6,-6,-6,-7,-7,-8,-8,-8,-9,-9,-10,-10,-11,-11,-11,-12,-12,-13,-13,-13,-14,-14,-15,-15,-16,-16,-16,-17,-17,-18,-18,-19,-19,-19,-20,-20,-21,-21,-21,-22,-22,-23,-23,-24,-24,-24,-25,-25,-26,-26,-26,-27,-27,-28,-28,-29,-29,-29,-30,-30,-31,-31,-31,-32,-32,-33,-33,-34,-34,-34,-35,-35,-36,-36,-37,-37,-37,-38,-38,-39,-39,-39,-40,-40,-41,-41,-42,-42,-42,-43,-43,-44,-44,-44,-45,-45,-46,-46,-47,-47,-47,-48,-48,-49,-49,-49,-50,-50,-51,-51,-52,-52,-52,-53,-53,-54,-54,-55,-55,-55,-56,-56,-57,-57,-57,-58,-58,-59,-59,-60,-60,-60,-61,-61,-62,-62,-62,-63,-63,-64,-64,-65,-65,-65,-66,-66,-67,-67,-67,-68,-68,-69,-69,-70,-70,-70,-71,-71,-72,-72,-73,-73,-73,-74,-74,-75,-75,-75,-76,-76,-77,-77,-78,-78,-78,-79,-79,-80,-80,-80,-81,-81,-82,-82,-83,-83,-83,-84,-84,-85,-85,-85,-86,-86,-87,-87,-88,-88,-88,-89,-89,-90,-90,-91,-91,-91,-92,-92,-93,-93,-93,-94,-94,-95,-95,-96,-96,-96,-97,-97,-98,-98,-98,-99,-99,-100,-100,-101,-101,-101,-102,-102,-103,-103,-104,-104,-104,-105,-105,-106,-106,-106,-107,-107},
{0,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-2,-2,-2,-2,-2,-2,-2,-2,-2,-2,-2,-2,-3,-3,-3,-3,-3,-3,-3,-3,-3,-3,-3,-3,-4,-4,-4,-4,-4,-4,-4,-4,-4,-4,-4,-4,-4,-5,-5,-5,-5,-5,-5,-5,-5,-5,-5,-5,-5,-6,-6,-6,-6,-6,-6,-6,-6,-6,-6,-6,-6,-7,-7,-7,-7,-7,-7,-7,-7,-7,-7,-7,-7,-7,-8,-8,-8,-8,-8,-8,-8,-8,-8,-8,-8,-8,-9,-9,-9,-9,-9,-9,-9,-9,-9,-9,-9,-9,-10,-10,-10,-10,-10,-10,-10,-10,-10,-10,-10,-10,-10,-11,-11,-11,-11,-11,-11,-11,-11,-11,-11,-11,-11,-12,-12,-12,-12,-12,-12,-12,-12,-12,-12,-12,-12,-13,-13,-13,-13,-13,-13,-13,-13,-13,-13,-13,-13,-14,-14,-14,-14,-14,-14,-14,-14,-14,-14,-14,-14,-14,-15,-15,-15,-15,-15,-15,-15,-15,-15,-15,-15,-15,-16,-16,-16,-16,-16,-16,-16,-16,-16,-16,-16,-16,-17,-17,-17,-17,-17,-17,-17,-17,-17,-17,-17,-17,-17,-18,-18,-18,-18,-18,-18,-18,-18,-18,-18,-18,-18,-19,-19,-19,-19,-19,-19,-19,-19,-19,-19,-19,-19,-20,-20,-20,-20,-20,-20,-20,-20,-20,-20,-20,-20,-20,-21,-21,-21,-21,-21,-21,-21,-21,-21}
};
//     b = 1.164*y+2.018*u-277;
//     g = 1.164*y-0.380*u-0.813*v+134;
//     r = 1.164*y+1.159*v-148;
static short int BUMap[3][256]={
{0,1,2,3,4,5,6,8,9,10,11,12,13,15,16,17,18,19,20,22,23,24,25,26,27,29,30,31,32,33,34,36,37,38,39,40,41,43,44,45,46,47,48,50,51,52,53,54,55,57,58,59,60,61,62,64,65,66,67,68,69,71,72,73,74,75,76,77,79,80,81,82,83,84,86,87,88,89,90,91,93,94,95,96,97,98,100,101,102,103,104,105,107,108,109,110,111,112,114,115,116,117,118,119,121,122,123,124,125,126,128,129,130,131,132,133,135,136,137,138,139,140,142,143,144,145,146,147,149,150,151,152,153,154,155,157,158,159,160,161,162,164,165,166,167,168,169,171,172,173,174,175,176,178,179,180,181,182,183,185,186,187,188,189,190,192,193,194,195,196,197,199,200,201,202,203,204,206,207,208,209,210,211,213,214,215,216,217,218,220,221,222,223,224,225,226,228,229,230,231,232,233,235,236,237,238,239,240,242,243,244,245,246,247,249,250,251,252,253,254,256,257,258,259,260,261,263,264,265,266,267,268,270,271,272,273,274,275,277,278,279,280,281,282,284,285,286,287,288,289,291,292,293,294,295,296},
{0,2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50,52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,98,100,102,104,106,108,110,113,115,117,119,121,123,125,127,129,131,133,135,137,139,141,143,145,147,149,151,153,155,157,159,161,163,165,167,169,171,173,175,177,179,181,183,185,187,189,191,193,195,197,199,201,203,205,207,209,211,213,215,217,219,221,224,226,228,230,232,234,236,238,240,242,244,246,248,250,252,254,256,258,260,262,264,266,268,270,272,274,276,278,280,282,284,286,288,290,292,294,296,298,300,302,304,306,308,310,312,314,316,318,320,322,324,326,328,330,332,334,337,339,341,343,345,347,349,351,353,355,357,359,361,363,365,367,369,371,373,375,377,379,381,383,385,387,389,391,393,395,397,399,401,403,405,407,409,411,413,415,417,419,421,423,425,427,429,431,433,435,437,439,441,443,445,448,450,452,454,456,458,460,462,464,466,468,470,472,474,476,478,480,482,484,486,488,490,492,494,496,498,500,502,504,506,508,510,512,514}
};
static short int GUMap[3][256]={
{0,1,2,3,4,5,6,8,9,10,11,12,13,15,16,17,18,19,20,22,23,24,25,26,27,29,30,31,32,33,34,36,37,38,39,40,41,43,44,45,46,47,48,50,51,52,53,54,55,57,58,59,60,61,62,64,65,66,67,68,69,71,72,73,74,75,76,77,79,80,81,82,83,84,86,87,88,89,90,91,93,94,95,96,97,98,100,101,102,103,104,105,107,108,109,110,111,112,114,115,116,117,118,119,121,122,123,124,125,126,128,129,130,131,132,133,135,136,137,138,139,140,142,143,144,145,146,147,149,150,151,152,153,154,155,157,158,159,160,161,162,164,165,166,167,168,169,171,172,173,174,175,176,178,179,180,181,182,183,185,186,187,188,189,190,192,193,194,195,196,197,199,200,201,202,203,204,206,207,208,209,210,211,213,214,215,216,217,218,220,221,222,223,224,225,226,228,229,230,231,232,233,235,236,237,238,239,240,242,243,244,245,246,247,249,250,251,252,253,254,256,257,258,259,260,261,263,264,265,266,267,268,270,271,272,273,274,275,277,278,279,280,281,282,284,285,286,287,288,289,291,292,293,294,295,296},
{0,0,0,1,1,1,2,2,3,3,3,4,4,4,5,5,6,6,6,7,7,7,8,8,9,9,9,10,10,11,11,11,12,12,12,13,13,14,14,14,15,15,15,16,16,17,17,17,18,18,18,19,19,20,20,20,21,21,22,22,22,23,23,23,24,24,25,25,25,26,26,26,27,27,28,28,28,29,29,30,30,30,31,31,31,32,32,33,33,33,34,34,34,35,35,36,36,36,37,37,37,38,38,39,39,39,40,40,41,41,41,42,42,42,43,43,44,44,44,45,45,45,46,46,47,47,47,48,48,49,49,49,50,50,50,51,51,52,52,52,53,53,53,54,54,55,55,55,56,56,56,57,57,58,58,58,59,59,60,60,60,61,61,61,62,62,63,63,63,64,64,64,65,65,66,66,66,67,67,67,68,68,69,69,69,70,70,71,71,71,72,72,72,73,73,74,74,74,75,75,75,76,76,77,77,77,78,78,79,79,79,80,80,80,81,81,82,82,82,83,83,83,84,84,85,85,85,86,86,86,87,87,88,88,88,89,89,90,90,90,91,91,91,92,92,93,93,93,94,94,94,95,95,96,96,96},
{0,0,1,2,3,4,4,5,6,7,8,8,9,10,11,12,13,13,14,15,16,17,17,18,19,20,21,21,22,23,24,25,26,26,27,28,29,30,30,31,32,33,34,34,35,36,37,38,39,39,40,41,42,43,43,44,45,46,47,47,48,49,50,51,52,52,53,54,55,56,56,57,58,59,60,60,61,62,63,64,65,65,66,67,68,69,69,70,71,72,73,73,74,75,76,77,78,78,79,80,81,82,82,83,84,85,86,86,87,88,89,90,91,91,92,93,94,95,95,96,97,98,99,99,100,101,102,103,104,104,105,106,107,108,108,109,110,111,112,113,113,114,115,116,117,117,118,119,120,121,121,122,123,124,125,126,126,127,128,129,130,130,131,132,133,134,134,135,136,137,138,139,139,140,141,142,143,143,144,145,146,147,147,148,149,150,151,152,152,153,154,155,156,156,157,158,159,160,160,161,162,163,164,165,165,166,167,168,169,169,170,171,172,173,173,174,175,176,177,178,178,179,180,181,182,182,183,184,185,186,186,187,188,189,190,191,191,192,193,194,195,195,196,197,198,199,199,200,201,202,203,204,204,205,206,207}
};
static short int RUMap[3][256]={
{0,1,2,3,4,5,6,8,9,10,11,12,13,15,16,17,18,19,20,22,23,24,25,26,27,29,30,31,32,33,34,36,37,38,39,40,41,43,44,45,46,47,48,50,51,52,53,54,55,57,58,59,60,61,62,64,65,66,67,68,69,71,72,73,74,75,76,77,79,80,81,82,83,84,86,87,88,89,90,91,93,94,95,96,97,98,100,101,102,103,104,105,107,108,109,110,111,112,114,115,116,117,118,119,121,122,123,124,125,126,128,129,130,131,132,133,135,136,137,138,139,140,142,143,144,145,146,147,149,150,151,152,153,154,155,157,158,159,160,161,162,164,165,166,167,168,169,171,172,173,174,175,176,178,179,180,181,182,183,185,186,187,188,189,190,192,193,194,195,196,197,199,200,201,202,203,204,206,207,208,209,210,211,213,214,215,216,217,218,220,221,222,223,224,225,226,228,229,230,231,232,233,235,236,237,238,239,240,242,243,244,245,246,247,249,250,251,252,253,254,256,257,258,259,260,261,263,264,265,266,267,268,270,271,272,273,274,275,277,278,279,280,281,282,284,285,286,287,288,289,291,292,293,294,295,296},
{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
{0,1,2,3,4,5,6,8,9,10,11,12,13,15,16,17,18,19,20,22,23,24,25,26,27,28,30,31,32,33,34,35,37,38,39,40,41,42,44,45,46,47,48,49,50,52,53,54,55,56,57,59,60,61,62,63,64,66,67,68,69,70,71,73,74,75,76,77,78,79,81,82,83,84,85,86,88,89,90,91,92,93,95,96,97,98,99,100,101,103,104,105,106,107,108,110,111,112,113,114,115,117,118,119,120,121,122,124,125,126,127,128,129,130,132,133,134,135,136,137,139,140,141,142,143,144,146,147,148,149,150,151,152,154,155,156,157,158,159,161,162,163,164,165,166,168,169,170,171,172,173,174,176,177,178,179,180,181,183,184,185,186,187,188,190,191,192,193,194,195,197,198,199,200,201,202,203,205,206,207,208,209,210,212,213,214,215,216,217,219,220,221,222,223,224,225,227,228,229,230,231,232,234,235,236,237,238,239,241,242,243,244,245,246,248,249,250,251,252,253,254,256,257,258,259,260,261,263,264,265,266,267,268,270,271,272,273,274,275,276,278,279,280,281,282,283,285,286,287,288,289,290,292,293,294,295}
};

/** RGB转灰度转换关系表
 *  Grey = (R*1 + G*2 + B*1) >> 2
    Grey= (R*2 + G*5 + B*1) >> 3
    Grey= (R*4 + G*10 + B*2) >> 4
    Grey = (R*9 + G*19 + B*4) >> 5
    Grey = (R*19 + G*37 + B*8) >> 6
    Grey= (R*38 + G*75 + B*15) >> 7
    Grey= (R*76 + G*150 + B*30) >> 8
    Grey = (R*153 + G*300 + B*59) >> 9
    Grey = (R*306 + G*601 + B*117) >> 10
    Grey = (R*612 + G*1202 + B*234) >> 11
    Grey = (R*1224 + G*2405 + B*467) >> 12
    Grey= (R*2449 + G*4809 + B*934) >> 13
    Grey= (R*4898 + G*9618 + B*1868) >> 14
    Grey = (R*9797 + G*19235 + B*3736) >> 15
    Grey = (R*19595 + G*38469 + B*7472) >> 16
    Grey = (R*39190 + G*76939 + B*14943) >> 17
    Grey = (R*78381 + G*153878 + B*29885) >> 18
    Grey =(R*156762 + G*307757 + B*59769) >> 19
    Grey= (R*313524 + G*615514 + B*119538) >> 20
 *
 */
//默认采用四位精度表示
//Grey= (R*4 + G*10 + B*2) >> 4
//Grey = (R*1224 + G*2405 + B*467) >> 12
//site 精确度
void Li_Arr_bgr_gray( LiArr* src,LiArr *dst,LONG width,LONG height,BYTE site)
{
  int x,y;
  switch (site)
  {

  case 0: //查表法实现灰度转换 12位
    for(x=0;x<height;x++)
      for(y=0;y<width;y++)
      {
        *((BYTE*)dst+width*x+y)=(YMap[2][*((BYTE*)src+3*width*x+3*y)]) //B
                                    +YMap[1][(*((BYTE*)src+3*width*x+3*y+1))] //G
                                      +YMap[0][(*((BYTE*)src+3*width*x+3*y+2))]; //R
      }
  break;

  case 4:
    for(x=0;x<height;x++)
      for(y=0;y<width;y++)
      {
        *((BYTE*)dst+width*x+y)=(*((BYTE*)src+3*width*x+3*y)*2) //B
                                    +(*((BYTE*)src+3*width*x+3*y+1)*10) //G
                                      +(*((BYTE*)src+3*width*x+3*y+2)*4)>>4; //R
      }
    break;

    case 8:
    for(x=0;x<height;x++)
      for(y=0;y<width;y++)
      {
        *((BYTE*)dst+width*x+y)=(*((BYTE*)src+3*width*x+3*y)*30) //B
                                    +(*((BYTE*)src+3*width*x+3*y+150)*10) //G
                                      +(*((BYTE*)src+3*width*x+3*y+2)*76)>>8; //R
      }
    break;

   case 16:
    for(x=0;x<height;x++)
      for(y=0;y<width;y++)
      {
        *((BYTE*)dst+width*x+y)=(*((BYTE*)src+3*width*x+3*y)*7472) //B
                                    +(*((BYTE*)src+3*width*x+3*y+150)*38469) //G
                                      +(*((BYTE*)src+3*width*x+3*y+2)*19595)>>16; //R
      }
    break;

  default:
    break;
  }

}

（3）统计概率，绘制直方图

//一张灰度直方图数据表
typedef struct tagLi_Hist
{
    float data[256];
}Li_Hist;

Li_Hist* Li_Create_Hist(float* data)
{
    Li_Hist* hist=(Li_Hist*)malloc(sizeof(Li_Hist));
    memcpy(hist->data,data,256*sizeof(float));
    return hist;
}


void Li_Destroy_Hist(Li_Hist* hist)
{
    free(hist);
}

/**
 * @name: Li_Print_Hist
 * @msg: 打印直方图
 * @param {Li_Hist* hist}
 * @return {*}
 */
LI_API
void Li_Print_Hist(Li_Hist* hist)
{
    printf("[ ");
    for(int i=0;i<256;i++)
    {
        printf("%f ",hist->data[i]);
    }
    printf(" ]");
}
/**
 * @name: Li_Visual_Hist
 * @msg: 直方图转化为图像
 * @param {Li_Hist* hist}
 * @return {Li_Image*}
 */
LI_API
Li_Image* Li_Visual_Hist(Li_Hist* hist)
{
    Li_Image* img=Li_Create_Image(256,256,LI_DEP_24U,LI_BMP_888);
    float max=0,div=0;
    for(int i=0;i<256;i++)
    {
        if(hist->data[i]>max)
            max=hist->data[i];
    }
    div=256/max;
    for(int i=0;i<256;i++)
    {
        Li_Line_H(img,0x0000FF,i,hist->data[i]*div);
    }
    return img;
}
/**
 * @name: Li_Get_Hist
 * @msg: 绘制直方图
 * @param {Li_Image* img 图像}
 * @return {Li_Hist* 直方图数据}
 */
LI_API 
Li_Hist* Li_Get_Hist(Li_Image* img)
{
   if(img->imgdepth!=LI_DEP_8U)return NULL;

   float* buffer;//存储0-255的数值出现的次数
   float* result;
   int length=img->width*img->height;
   //将申请的地址全部初始化为0
   buffer=malloc(256*sizeof(float));
   result=malloc(256*sizeof(float));
   memset(buffer,0,256*4);
   memset(result,0,256*4);

   for(int i=0;i<length;i++)
   {
      BYTE off=*((BYTE*)img->data+i);
      buffer[off]++;
   }

   for(int i=0;i<256;i++)
   {
      result[i]=buffer[i]/length;
   }
   Li_Hist* hist=Li_Create_Hist(result);
   return hist;
}

（4）直方图均衡化算法实现

/**
 * @name: Li_Normalize_Hist
 * @msg: 直方图均衡化
 * @param {Li_Image* img}
 * @return {*}
 */
LI_API
Li_Image* Li_Normalize_Hist(Li_Image* img)
{
    Li_Image* dst=Li_Copy_Image(img);
    Li_Hist* Hist= Li_Get_Hist(img);
    float Max,Min;
    float sum[256];
    BYTE out[256];//对于源灰度值产生进行新的映射表
    BYTE* buf=malloc(img->width*img->height*sizeof(BYTE));
    //找到原图灰度值中的最大值和最小值 
    //一般而言应该是0-255
    for(int i=1;i<img->width*img->height;i++)
    {
        if(*((BYTE*)img->data+i)>Max)
        {
            Max=*((BYTE*)img->data+i);
        }
         if(*((BYTE*)img->data+i)<Min)
        {
            Min=*((BYTE*)img->data+i);
        }
    }
    BYTE* inaddr;
    float* data=Hist->data;
    //计算累计概率和
    sum[0]=*data;
    for(int i=1;i<=255;i++)
    {
       sum[i]=sum[i-1]+*(data+i);
       out[i]=(BYTE)(sum[i]*(Max-Min));//获得一张新的灰度值表
    }

   for(int x=0;x<dst->width;x++)
   for(int y=0;y<dst->height;y++)
   {
        inaddr=dst->at(dst,x,y);
        BYTE temp=*inaddr;
       *(inaddr)=out[temp];
   }
   return dst;
}

（四）效果测试

原图

图像加强后

我们可以明显看到图像清晰度的增强。

（五）局限性分析

这张加强显然不是万能的，在进行一幅图片的加强的时候就出现了非常极端的情况。

非常明显当原图亮度过高，或者在某一灰度值出现次数太多，就一定会出现这种失真。

2021年7月6日2021年7月6日

【数字图像处理】图像几何变换之图像的极坐标变化展开鱼眼图

（一）基础知识

极坐标变换及其反变换的关键在于，根据极坐标变换前的图像（我们称为“方图”）确定极坐标变换后的图像（我们称为“圆图”）上每个像素点的像素值。也即是找到“圆图”和“方图”间几何坐标的对应关系。

1、极坐标变换

原理：
如下图所示，实现极坐标变换的关键即在于找到圆图上任一点P(i,j)，在方图上对应的点p(m,n)，然后通过插值算法实现圆图上所有像素点的赋值。
方图上，其行列数分别为M、N，方图上的每一列对应为圆图上的每条半径，半径方向存在着一个长度缩放因子delta_r = M/R，圆周方向被分为N等分，即角度因子为delta_t = 2π/N；
圆图上，图像坐标（i,j）和世界坐标（x,y）有着如下变换关系：x = j – R, y = R – i；
那么，图中P点半径长度为r = sqrt(xx + yy)，角度theta = arctan(y/x)；
圆图上点P在方图上对应行数为r/delta_r；
圆图上点P在方图上对应的列数n = thata/delta_t。

图像变换过程可以参考

（二）软件设计

因为这个代码时应用于嵌入式平台必须考虑到计算速度的问题，所以这里我们自己实现三角函数的近似计算缺点在于，边界点可能会出现失真。

/**
 * @fn  float fastSin(float x)
 *
 * @brief   自定义快速变换 sin  cos  函数  定义 而外精度 更高拟合效果 参考链接
 *          https://www.cnblogs.com/sun11086/archive/2009/03/20/1417944.html
 *
 * @author  IRIS_Chen
 * @date    2019/6/17
 *
 * @param   x   The x coordinate
 *
 * @return  A float
 */
//本质上是利用了一个已经拟合好的二次函数近似三角函数
float fastSin(float x)
{
    float y;
    // 限定 x 在 -Pi  到 pi
    while (x < - PI)
    {
        x += (float)(2 * PI);
    }
    while (x > PI)
    {
        x -= (float)(2 * PI);
    }

    const float B = 1.2732; // 4 / CV_PI;
    const float C = -0.4053; // -4 / (CV_PI*CV_PI);
    if(x>0)
    {
    y = B * x + C * x * x;
    }
    else
    {
     y = -1*B * x + C * x * x;
    }
    return y;
}


/**
 * @fn  float fastCos(float x)
 *
 * @brief   Fast cosine
 *
 * @author  IRIS_Chen
 * @date    2019/6/17
 *
 * @param   x   The x coordinate
 *
 * @return  A float
 */
float fastCos(float x)
{
    return fastSin(x + 1.5707);
}

Mat creatMapMat(Mat src, 
                 int rows_c,
                 int cols_c,
                 double startdelta)
{
    Mat dst;
    int i,j;
    u8* inaddr;
    u8* outaddr;
    int polar_d =src.width;
    double polar_r = polar_d / 2.0;
    printf("1");
    dst=create("..\\picture\\test.bmp",cols_c,rows_c,3);
    double delta_r = polar_r / rows_c; //半径因子
    double delta_t = 2.0*PI / cols_c;  //角度因子
    double center_polar_x = (polar_d - 1) / 2.0;
    double center_polar_y = (polar_d - 1) / 2.0;
    printf("2");
    for (i = 0; i < cols_c; i++)
    {
        double theta_p = i * delta_t+startdelta; //方图第i列在圆图对应线的角度
        double sin_theta = fastSin(theta_p);
        double cos_theta = fastCos(theta_p);

        for (int j = 0; j < rows_c; j++)
        {
            double temp_r = j * delta_r; //方图第j行在圆图上对应的半径长度

            int polar_x = (int)(center_polar_x + temp_r * cos_theta);
            int polar_y = (int)(center_polar_y - temp_r * sin_theta);
            if(i<dst.width&&j<dst.highth&&polar_x<src.width&&polar_y<=src.highth)
            {
            inaddr=at(&dst,i,j);
            outaddr=at(&src,polar_x,polar_y);
            *inaddr=*outaddr;
            *(inaddr+1)=*(outaddr+1);
            *(inaddr+2)=*(outaddr+2);
            }
        }
    }
    return dst;
}

(三)应用举例

/*************************************************
Copyright © Yueyang Co. Ltd. 2019-2029. All rights reserved.
File name: cv.h
Author： Yueyang
Version: V1.0
Description: LiteCV运行主函数
Others: 
Log: 11.3 Yueyang
*************************************************/

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <malloc.h>

#include "bmp.h"
#include "cv.h"
#include "GeoTrans.h"
#include "PointOr.h"
#include "BasicGui.h"

int main()
{
     Mat src;
     Mat_Init();
     src=load("..\\picture\\hole.bmp");

     Mat dst=dst=creatMapMat(src, 500,500,PI/4);

     save("..\\picture\\test.bmp",&dst);

     show(&dst);

     destory(&src);
     destory(&dst);
      return 0; 
}

原图：
这是一张医学中使用的人的血管内壁照片：

变换后：

（四）写在后面

因为LiteCV项目才刚刚写了一个开头，代码中有错误的地方还望指出。我已经将项目同步到了github，我会实时更新这个代码仓库。
项目github地址：
LITECV

(一)Seetaface2 基本概念

1 图像

1.1 结构定义

1.2 使用示例

2. 人脸检测和关键点定位

2.1 人脸检测器

2.2 人脸关键点定位器

3. 人脸特征提取和对比

3.1 人脸特征提取

(二)代码实现

(三)效果

(四)写在后面

(一)关于QR二维码

一：什么是二维码

二：什么是QR二维码

三：将数据编码成QR码的流程

(二)编译QRencode

(三)使用libqrencode.a

(四)效果

(五)写在后面

(一)Hough圆检测

程序设计

（1） 因为如果直接进行Hough圆的投票的话，我们需要一个3维的表保存行，列，角度信息。我们将这个投票过程分成两个步骤。

（2） 首先完成对于固定半径的圆的投票。然后在对每一个半径的圆的投票进行比较。

（3） 对一个半径范围内的所有圆进行一次（1）中的操作，然后，从中选取票数最高的圆，那么这个圆就是我们想要的圆了。

（4） 具体程序请参考Litecv/Imgproc/li_canny.c

(二) Hough直线检测

(三)代码实现

(四)效果展示

(五)写在后面

（一）边缘检测步骤

（二）图像的梯度与方向角计算

（1）sobel算子

（2） Prewitt算子

（3） Robert算子

（4）三种算子效果比较

（三）非极大值抑制

（四）图像双阈值化与边缘连接

（五）代码实现

li_canny.c

main.c

（六）写在后面

(一)图像卷积

1. 图像卷积

2. 数字信号处理中的卷积

3 数字图像处理中的卷积

（二）图像卷积实现各种形态学运算

腐蚀

膨胀

形态学梯度

开运算

闭运算

顶帽

黑帽

雕版

锐化

li_conv.c

main.c

(三)效果展示

原图

腐蚀

膨胀

形态学梯度

开运算

闭运算

顶帽

黑帽

雕版

锐化

（四）写在后面

（一）均值滤波

（二） 高斯滤波

（三） 中值滤波

（四）选择滤波算法

（五）代码实现

li_smooth.c

main.c

（六）写在后面

LiteCV 使用说明

（一）写在前面

（1）因为如果直接进行Hough圆的投票的话，我们需要一个3维的表保存行，列，角度信息。我们将这个投票过程分成两个步骤。

（2）首先完成对于固定半径的圆的投票。然后在对每一个半径的圆的投票进行比较。

（3）对一个半径范围内的所有圆进行一次（1）中的操作，然后，从中选取票数最高的圆，那么这个圆就是我们想要的圆了。

（4）具体程序请参考Litecv/Imgproc/li_canny.c

（二）高斯滤波

（三）中值滤波

第一步滤波

第二步梯度化与边缘检测

第三步检测圆后获取感兴趣区域

第四步直线检测与读数